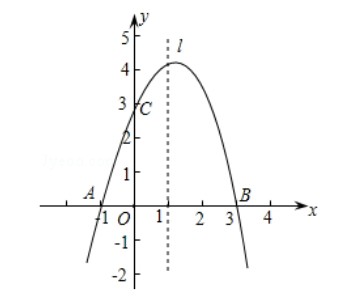
1. 已知抛物线y=ax-+bx+c经过A (- 1，0)、B (3, 0)、C (0, 3)三点，直线1是抛物线的对称轴.

　　(1)求抛物线的函数关系式;

　　(2)设点P是直线1上的一个动点，当△PAC的周长最小时，求点P的坐标;

　　(3)在直线1上是否存在点M，使△MAC为等腰三角形?若存在，直接写出所有符合条件的点M的坐标;若不存在，请说明理由。

　　参考答案：

　　(1)抛物线的解析式: y=x²+2x+3.

　　(2)连接BC，直线BC与直线1的交点为P;

　　∵点A、B关于直线1对称，∴PA=PB，∴BC=PC+PB=PC+PA

　　设直线BC的解析式为y=kx+b (k≠0)，将B (3，0)，C (O，3)代入上式，得:

　　3k+b=0;b=3

　　解得:

　　k=- 1;b=3

　　∴直线BC的函数关系式y=-x+3;当x=1时，y=2，即P的坐标(1, 2).

　　(3)抛物线的对称轴为: x=-b/2a=1，设M(1,m)，已知A(-1,0)、C(0，3)，则:

　　MA²=m²+4，MC²= (3 -m) ²+1=m²- 6m+10，AC²=10;

　　①若MA=MC，则MA²=MC²,得: m²+4=m²- 6m+10,得: m=1;

　　②若MA=AC，则MA²-=AC²，得: m²+4=10， 得: m=+√6;

　　③若MC=AC，则MC²=Ac²，得: m²- 6m+10=10，得: m1=0, m2=6;

　　当m=6时，M、A、C三点共线，构不成三角形，不合题意，故舍去;

　　综上可知，符合条件的M点，且坐标为M (1,√6) (1，-√6) (1，1) (1, 0).