一、选择题(每题3分,共45分)

　　1. 下列各式，，，中，分式的个数是(　　)

　　(A)0　　　 (B)1　　　 (C)2　　　(D) 3

　　2.“从布袋中取出一个红球的概率为0”，这句话的含义是(　　 )

　　(A) 布袋中红球很少　　 (B) 布袋中没有球

　　(C) 布袋中没有红球　　　(D) 不能确定

　　3.下列计算正确的是(　 )

　　(A) =0 　(B)=-15　 (C)(D)  

　　4. 如图，已知O是线段AC和BD的中点，要说明△ABO≌△CDO，以下回答最合理的是(　　 )

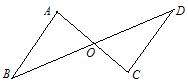
　　(A) 添加条件∠A=∠C

　　(B) 添加条件AB=CD

　　(C) 不需要添加条件

　　(D) △ABO和△CDO不可能全等

　　5.下列语句中表示命题的是(　 )

　　(A) 画一条线段.　　　　　　　　　　 (B)　作线段AB的垂直平分线.

　　(C) 等边三角形是中心对称图形吗?　　(D)　平行四边形对角线相等.

　　6.在下列考察中，是抽样调查的是(　 )

　　(A) 了解全校学生人数　　　　 (B) 调查某厂生产的鱼罐头质量

　　(C) 调查杭州市出租车数量　　 (D) 了解全班同学的家庭经济状况

　　7. 已知两圆的半径分别为8和5，圆心距为5，那么这两圆的位置关系是(　　 )

　　(A) 内切　　 (B)　外切　　　 (C)　 相交　　 (D)　 外离

　　8. 如图，已知∠BPC=50°，∠ABC=60°，则∠ACB是(　　 )

　　(A) 40°　　　 (B)　50°　　　　 (C)　60°　　 (D)　70°

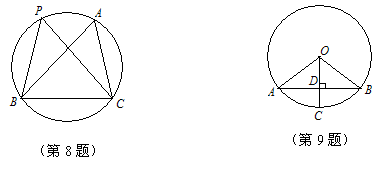
　　9. 如图，已知⊙O中，半径OC垂直于弦AB，垂足为D，若OD=3，OA=5，则AB的长为(　　)

　　(A) 2　　　　 (B) 4　　　　(C) 6　　　　 (D) 8

　　10. 若方程的一个根为，则k及另一个根的值为(　 )

　　(A) 7 ，3　　(B)　-7，3　　　 (C)　 ，6　 (D)　，6

　　11. 下面几个抽样调查选取样本的方法合理的有(　　 )

　　(1)为调查我国的人均国民收入状况，只在杭州市进行调查;

　　(2)为估计杭州市中考数学成绩，抽取所有学号尾数是0和5中考学生进行调查;

　　(3)为调查杭州市中学生的健康状况，共调查10名中学生的健康状况.

　　(A) 0个　　　 (B) 1个　　　 (C) 2个　　　(D) 3个

　　12.方程的左边配成完全平方后所得方程为　　　　(　　 )

　　(A)　　 (B) (C) 　　 (D)

　　13. 10个人去钓鱼，共钓到3条鱼，假设每个人钓到鱼的可能性相同，那么这3条鱼由同一个人钓到的概率是(　　　)

　　(A)　 (B)　 (C)　 (D)  

　　14. 一块等边三角形的木板，边长为1，现将木板沿水平线翻滚(如图)，那么B点从开始至结束所走过的路径长度为(　　　)

 

 

 

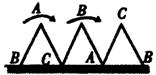
　　 (A)(B)(C) 4　　　(D)2+

　　15.某厂生产一种药品，原来每瓶的成本是100元，由于提高生产过程的科技含量，连续两次降低成本，现在的成本是81元.则平均每次降低成本 (　　)

　　(A)8.5%　　(B)9%　　(C)9.5%　　(D)10%

　　二、填空题(每题4分，共20分)

　　16.如果分式有意义，那么的取值范围是　　 ▲　　 .

　　17.方程的解是　　 ▲　　 .

　　18.一圆锥的底面半径为2cm，母线长为5cm，则此圆锥的侧面积为　　▲　　.

　　19.近年来，我国长江、黄河流域植被遭到破坏，导致土地沙化，洪涝灾害时有发生.沿黄某地区为积极响应和支持“保护母亲河”的倡议，在2000年建立了长100km，宽0.5km的防护林.今年，有关部门为统计这一防护林约有多少棵树，从中选出10块(每块长1km，宽0.5km)统计，数量如下(单位：棵)：

　　65110　63200　64600　64700　67300　63300　65100　66600　62800　65500

　　根据以上数据可知这一防护林约有　　　 ▲　 棵树.

20. 如图，这是一个滚珠轴承的示意图，其中内、外圆

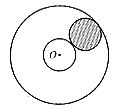
　　的半径分别为2和6，如果在内、外圆之间放半径为2

　　的滚珠(有阴影的圆表示滚珠)，那么在内、外圆之间最

　　多可以放____▲___个滚珠.

　　三.解答题(本题有6小题，共55分)

　　21.(9分)如图，已知∠ABC，求作：

　　(1)∠ABC的平分线BD(写出作法，并保留作图痕迹);

　　(2)在BD上任取一点P，作直线PQ，使PQ⊥AB(不写作法，保留作图痕迹).

　　22.计算(10分)(本题有3小题，分值不同，请任选2题计算，多答不加分)

　　(1)(4分)　　　　

　　(2)(5分)

　　 (3)(5分)

　　23.解方程(10分)(本题有3小题，分值不同，请任选2题作答，多答不加分)

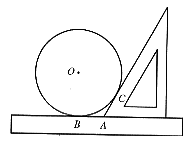
　　(1)(4分)　　　　　　　(2)(5分) (3)(5分)  

　　24.(7分) 已知：如图，为测量一个圆的半径，采用了下面的方法：将圆平放在一个平面上，用一个含有30°角的三角板和一把直尺，按图示的方式测量(此时，⊙O与三角板和直尺分别相切，切点分别为点C、点B)，若量得AB=5cm，试求圆的半径以及的弧长。

 

　

 

 

 

　　25.(10分)已知方程

　　(1)求此方程的解;

　　(2)联系生活实际，编写一道能用上述方程解决的应用题(不需解答).

　　26.(本题满分9分)已知：等边△ABC和点P，设点P到△ABC三边AB、AC、BC的距离分别为h1、h2、h3，△ABC的高为h.若点P在一边BC上(如图26—1)，此时h3=0，可得结论：h1+h2+h3=h.

　　请直接应用上述结论或其它方法解决下列问题：当点P在△ABC内(如图26—2)、点P在△ABC外(如图26—3)这两种情况时，上述结论是否成立?若成立，请给予证明;若不成立，h1、h2、h3与h之间又有怎样的关系?请写出你的猜想(不需要证明)。