一、选择题(本题共 30 分，每小题 3 分)

　　1.春节假期，北京市推出了庙会休闲娱乐、传统文化展演、游园赏景赏花、冰雪项目体验等精品文化活动，共接待旅游总人数 9 608 000 人次，将 9 608 000 用科学记数法表示为

　　(A) 9608 ´103 (B) 960.8 ´104

　　(C) 96.08 ´105

　　(D) 9.608 ´106

　　2.在数轴上，实数 a，b 对应的点的位置如图所示，且这两个点关于原点对称，下列结论中，正确的是(    )

　　(A) a + b = 0

　　(B) a - b = 0

　　(C) a < b

　　(D) ab>0

　　3.如图，AB∥CD，DA⊥CE 于点 A.若∠EAB=55°，则∠D 的度数为(      )

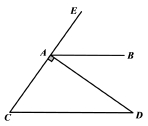
　　(A)25°

　　(B)35°

　　(C)45°

　　(D)55°

　　4.右图是某几何体的三视图，该几何体是

　　(A)三棱柱

　　(B)长方体

　　(C)圆锥

　　(D)圆柱

　　5.若正多边形的一个外角是 40°，则这个正多边形是

　　(A)正七边形

　　(C)正九边形

　　(B)正八边形

　　(D)正十边形

　　6.用配方法解一元二次方程 x　- 6 x - 5 = 0 ，此方程可化为

　　(A)( x - 3)2= 4

    (B)( x - 3)2= 14

　　(C)( x - 9)2= 4

　　(D)( x - 9)2= 14

　　7.如图，小明在地面上放了一个平面镜，选择合适的位置，刚好在平面镜中看到旗杆的顶部，此时小明与平面镜的水平距离为 2m，旗杆底部与平面镜的水平距离为 16m.若小明的眼睛与地面距离为 1.5m，则旗杆的高度为(单位：m)

　　

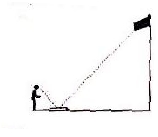
　　　　(A) (B)9 (C)12 (D)

　　8.某商店举行促销活动，其促销的方式是“消费超过 100 元时，所购买的商品按原价打 8折后，再减少 20 元” .若某商品的原价为 x 元(x>100)，则购买该商品实际付款的金额(单位：元)是

　　(A) 80%x - 20 (B) 80% ( x - 20)

　　(C) 20%x - 20 (D) 20% ( x - 20)

　　9.某校合唱团有 30 名成员，下表是合唱团成员的年龄分布统计表：对于不同的 x，下列关于年龄的统计量不会发生改变的是

　　(A)平均数、中位数

　　(C)众数、中位数

　　(B)平均数、方差

　　(D)众数、方差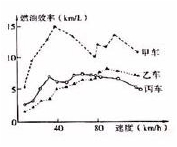

　　10.汽车的“燃油效率”是指汽车每消耗 1 升汽油行驶的里程数.“燃油效率”越高表示汽车每消耗 1 升汽油行驶的里程数越多;“燃油效率”越低表示汽车每消耗 1 升汽油行驶的里程数越少.右下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况，下列说法中，

　　正确的是

　　(A)以相同速度行驶相同路程，三辆车中，甲车消耗汽油最多

　　(B)以低于 80km/h 的速度行驶时，行驶相同路程，三辆车中，乙车消耗汽油最少

　　(C)以高于 80km/h 的速度行驶时，行驶相同路程，丙车比乙车省油

　　(D)以 80km/h 的速度行驶时，行驶 100 公里，甲车消耗的汽油量约为 10 升 

　　二、填空题(本题共 18 分，每小题 3 分)

　　11.分解因式：ax2 - 2ax+a=________.

　　12.若函数的图像经过点 A(1，2)，点 B(2，1)，写出一个符合条件的函数表达式_________.

　　13.下表记录了一名球员在罚球线上罚篮的结果：

　　这名球员投篮一次，投中的概率约是

　　14.如图，四边形 ABCD 是⊙O 内接四边形，若∠BAC=30°，∠CBD=80°，则∠BCD 的度

　　数为_________________.

　　第 14 题图

　　第 15 题

　　15.在平面直角坐标系 xOy 中，以原点 O 为旋转中心，将△AOB 顺时针旋转 90°得到

　　△A'OB'，其中点 A'与点 A 对应，点 B'与点 B 对应.若点 A( - 3，0)，B( - 1， 2)，

　　则点 A'的坐标为_______________，点 B'的坐标为________________.

　　16.下面是“经过已知直线外一点作这条直线的平行线”的尺规作图过程.

　　已知：如图 1，直线 l 和直线 l 外一点 P.

　　求作：直线 l 的平行直线，使它经过点 P.

　　作法：如图 2.

　　(1) 过点 P 作直线 m 与直线 l 交于点 O;

　　(2) 在直线 m 上取一点 A(OA

　　长为半径画弧，与直线 l 交于点 B;

　　(3) 以点 P 为圆心，OA 长为半径画弧，交直线 m 于点

　　C，以点 C 为圆心，AB 长为半径画弧，两弧交于点

　

　　所以直线 PD 就是所求作的平行线.

　　请回答：该作图的依据是

　　三、解答题(本题共 72 分，第 17-26 题，每小题 5 分，第 27 题 7 分，第 28 题 7 分，第 29

　　题 8 分)解答应写出文字说明、演算步骤或证明过程.

　　è 2 ø　-1)0- 2sin60O + 3 - 2ïx + 72æ 1è y1 öx øx 2 - 2 xy + y 2x 2 y的值.

　　20. 如图，在△ABC 中，BC 的垂直平分线交 BC 于点 D，交 AB 延长线于点 E，连接 CE.

　　求证：∠BCE=∠A+∠ACB.

　　21.某科研小组计划对某一品种的西瓜采用两种种植技术种植.在选择种植技术时，该科研

　　小组主要关心的问题是：西瓜的产量和产量的稳定性，以及西瓜的优等品率. 为了解这两种

　　种植技术种出的西瓜的质量情况，科研小组在两块自然条件相同的试验田进行对比试验，并

　　从这两块实验田中各随机抽取 20 个西瓜，分别称重后，将称重的结果记录如下：

　　表 1

　　表 2

　　甲种种植技术种出的西瓜质量统计表

　　乙种种植技术种出的西瓜质量统计表

　　回答下列问题：

　　(1)若将质量为 4.5~5.5(单位：kg)的西瓜记为优等品，完成下表：

　　(2)根据以上数据，你认为该科研小组应选择哪种种植技术，并请说明理由.

　 22. 在平面直角坐标系 xOy，直线 y=x-1 与 y 轴交于点 A，与双曲线 y=kx交于点 B(m，2).

　　(1)求点 B 的坐标及 k 的值;

　　(2)将直线 AB 平移，使它与 x 轴交于点 C，与 y 轴交于点 D，若△ABC 的面积为 6，求直

　　线 CD 的表达式.

　　.如图，在23ABCD 中，对角线 BD 平分∠ABC，过点 A 作 AE//BD，交 CD 的延长线于点

　　E，过点 E 作 EF⊥BC，交 BC 延长线于点 F.

　　(1)求证：四边形 ABCD 是菱形;

　　(2)若∠ABC=45°，BC=2，求 EF 的长.

　 24. 汽车保有量是指一个地区拥有车辆的数量，一般是指在当地登记的车辆.进入 21 世纪

　　以来，我国汽车保有量逐年增长.下图是根据中国产业信息网上的有关数据整理的统计图.

　　2007—2015 年全国汽车保有量及增速统计图

　　根据以上信息，回答下列问题：

　　(1)2016 年汽车保有量净增 2200 万辆，为历史最高水平，2016 年汽车的保有量为万辆，与 2015 年相比，2016 年的增长率约为%;

　　(2)从 2008 年到 2015 年，

　　(3)预估 2020 年我国汽车保有量将达到

　　年全国汽车保有量增速最快;

　　万辆，预估理由是

　　25.如图，AB 为⊙O 的直径，C 为⊙O 上一点，过点 C 作⊙O 的切线，交 BA 的延长线交

　　于点 D，过点 B 作 BE⊥BA，交 DC 延长线于点 E，连接 OE，交⊙O 于点 F，交 BC 于点 H，

　　连接 AC.

　　(1)求证：∠ECB=∠EBC;

　　(2)连接 BF，CF，若 CF=6，sin∠FCB=求 AC 的长.

　　26.阅读下列材料：

　　某种型号的温控水箱的工作过程是：接通电源后，在初始温度 20℃ 下加热水箱中

　　的水;当水温达到设定温度 80℃ 时，加热停止;此后水箱中的水温开始逐渐下降，当

　　下降到 20℃ 时，再次自动加热水箱中的水至 80℃ 时，加热停止;当水箱中的水温下

　　降到 20℃ 时，再次自动加热，……，按照以上方式不断循环.

　　小明根据学习函数的经验，对该型号温控水箱中的水温随时间变化的规律进行了探

　　究.发现水温 y 是时间 x 的函数，其中 y(单位：℃ )表示水箱中水的温度.x(单位：min)

　　表示接通电源后的时间.

　　下面是小明的探究过程，请补充完整：

　　(1)下表记录了 32min 内 14 个时间点的温控水箱中水的温度 y 随时间 x 的变化情况

　　m 的值为

　　(2)①当 0≤x≤4 时，写出一个符合表中数据的函数解析式当 4

　　②如图，在平面直角坐标系 xOy 中，描出了上表中部分数据对应的点，根据描出的

　　点，画出当 0≤x≤32 时，温度 y 随时间 x 变化的函数图象：

　　(3) 如果水温 y 随时间 x 的变化规律不变，预测水温第 8 次达到 40℃时，距离接通电源　min.

　　27.在平面直角坐标系 xOy 中，二次函数 y=mx2 - (2m + 1)x + m - 5 的图象与 x 轴有两个公

　　共点.

　　(1)求 m 的取值范围;

　　(2)若 m 取满足条件的最小的整数，

　　①写出这个二次函数的解析式;

　　②当 n ≤ x ≤ 1 时，函数值 y 的取值范围是 - 6 ≤ y ≤ 4 - n，求 n 的值;

　　③将此二次函数平移，使平移后的图象经过原点 O.设平移后的图象对应的函数表达式为

　　y=a(x - h)2 + k，当 x < 2 时，y 随 x 的增大而减小，求 k 的取值范围.

　　.在28ABC 中，AB=BC，BD⊥AC 于点 D.

　　(1)如图 1，当∠ABC=90°时，若 CE 平分∠ACB，交 AB 于点 E，交 BD 于点 F.

　　①求证：△BEF 是等腰三角形;

　　②求证：BD=12(BC + BF);

　　(2)点 E 在 AB 边上，连接 CE.若 BD=12(BC + BE)，在图 2 中补全图形，判断∠ACE 与

　　∠ABC 之间的数量关系，写出你的结论，并写出求解∠ACE 与∠ABC 关系的思路.

　　　29.在平面直角坐标系 xOy 中，若点 P 和点 P1 关于 y 轴对称，点 P1 和点 P2 关于直线 l 对称，

　　则称点 P2 是点 P 关于 y 轴，直线 l 的二次对称点.

　　(1)如图 1，点 A(-1 , 0).

　　①若点 B 是点 A 关于 y 轴，直线 l1: x=2 的二次对称点，则点 B 的坐标为

　　②若点 C(-5 , 0)是点 A 关于 y 轴，直线 l2:x=a 的二次对称点，则 a 的值为

　　③若点 D( 2 , 1)是点 A 关于 y 轴，直线 l3 的二次对称点，则直线 l3 的表达式

　　为

　　　(2)如图 2，⊙O 的半径为 1.若⊙O 上存在点 M，使得点 M'是点 M 关于 y 轴，直线 l4:x=b的二次对称点，且点 M'在射线 y =33x(x ³ 0) 上，b 的取值范围是

　　(3)E(t，0)是 x 轴上的动点，⊙E 的半径为 2，若⊙E 上存在点 N，使得点 N'是点 N关于 y 轴，直线 l5: y = 3x + 1的二次对称点，且点 N'在 y 轴上，求 t 的取值范围.