三、解答题(写出必要的计算步骤，只写最后结果不得分，共70分)

　　17.(10分)已知p：方程+=1所表示的曲线为焦点在x轴上的椭圆;q：实数t满足不等式t2-(a-1)t-a<0.

　　(1)若p为真，求实数t的取值范围;

　　(2)若p是q的充分不必要条件，求实数a的取值范围.

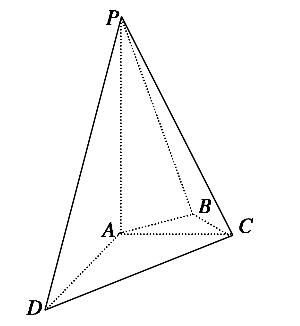
　　解：(1)∵方程+=1所表示的曲线为焦点在x轴上的椭圆，∴3-t>t+1>0.解得-1

　　(2)∵p是q的充分不必要条件，∴{t|-1-1时，不等式的解集为{t|-11.②当a=-1时，不等式的解集为∅，不满足题意.③当a<-1时，不等式的解集为{t|a1.

　　18.(12分)

　　如图，三棱柱

　　ABC—A1B1C1中，CA=CB，AB=AA1，∠BAA1=60°.

　　(1)证明：AB⊥A1C;

　　(2)若平面ABC⊥平面AA1B1B，AB=CB，求直线A1C与平面BB1C1C所成角的正弦值.

　　解：(1)取AB的中点O，连接OC，OA1，A1B.

　　因为CA=CB，所以OC⊥AB.

　　由于AB=AA1，∠BAA1=60°，故△AA1B为等边三角形，所以OA1⊥AB.

　　因为OC∩OA1=O，所以AB⊥平面OA1C.

　　又A1C⊂平面OA1C，故AB⊥A1C.

　　(2)由(1)知OC⊥AB，OA1⊥AB.

　　又平面ABC⊥平面AA1B1B，交线为AB，所以OC⊥平面AA1B1B，故OA，OA1，OC两两相互垂直.

　　以O为坐标原点，的方向为x轴的正方向，||为单位长，建立如图所示的空间直角坐标系O-xyz.

　　由题设知A(1,0,0)，A1(0，，0)，C(0,0，)，B(-1,0,0).

　　则=(1,0，)，==(-1，，0)，=(0，-，).

　　设n=(x，y，z)是平面BB1C1C的法向量，

　　则，即，

　　可取n=(，1，-1).

　　故cosn，==-.

　　所以A1C与平面BB1C1C所成角的正弦值为.

　　19.(12分)已知定点F(0,1)和定直线l1：y=-1，过定点F与直线l1相切的动圆圆心为点C.

　　(1)求动点C的轨迹方程;

　　(2)过点F的直线l2交轨迹于两点P，Q，交直线l1于点R，求·的最小值.

　　解：(1)由题意，点C到点F的距离等于它到l1的距离，∴点C的轨迹是以F为焦点，l1为准线的抛物线.∴所求轨迹的方程为x2=4y.

　　(2)由题意，直线PQ的斜率存在，且不为0，设直线l2的方程为y=kx+1(k≠0)，与抛物线方程联立消去y，得x2-4kx-4=0.记P(x1，y1)，Q(x2，y2)，则x1+x2=4k，x1x2=-4.易得点R的坐标为，∴·=·=+(kx1+2)(kx2+2)=(1+k2)x1x2+(x1+x2)++4=-4(1+k2)+4k++4=4+8，∵k2+≥2，当且仅当k2=1时取到等号，∴·≥4×2+8=16，即·的最小值为16.

　　20.(12分)设F1，F2分别是椭圆：+=1(a>b>0)的左、右焦点，过F1倾斜角为45°的直线l与该椭圆相交于P，Q两点，且|PQ|=a.

　　(1)求该椭圆的离心率.

　　(2)设点M(0，-1)满足|MP|=|MQ|，求该椭圆的方程.

　　解：(1)直线PQ斜率为1，

　　设直线l的方程为y=x+c，

　　其中c=.

　　设P(x1，y1)，Q(x2，y2)，则P，Q两点坐标满足方程组化简得(a2+b2)x2+2a2cx+a2(c2-b2)=0，

　　则x1+x2=，x1x2=.

　　所以|PQ|=|x2-x1|

　　==a.

　　得a=，故a2=2b2，

　　所以椭圆的离心率e===.

　　(2)设PQ的中点为N(x0，y0)，

　　由(1)知x0===-c，

　　y0=x0+c=.

　　由|MP|=|MQ|得kMN=-1.

　　即=-1，

　　得c=3，从而a=3，b=3.

　　故椭圆的方程为+=1.

　　21.(12分)

　　如图所示，在四棱锥P-ABCD中，PA⊥平面ABCD，AC⊥AD，AB⊥BC，∠BAC=45°，PA=AD=2，AC=1.

　　(1)求证：PC⊥AD;

　　(2)求二面角A-PC-D的正弦值;

　　(3)设E为棱PA上的点，满足异面直线BE与CD所成的角为30°，求AE的长.

　　解：如右图所示，以点A为原点建立空间直角坐标系，依题意得A(0,0,0)，D(2,0,0)，C(0,1,0)，B，P(0,0,2).

　　(1)证明：=(0,1，-2)，=(2,0,0)，所以·=0，所以PC⊥AD.

　　(2)解：=(0,1，-2)，=(2，-1,0).

　　设平面PCD的法向量为n=(x，y，z)，

　　则即不妨令z=1，则x=1，y=2，故平面PCD的一个法向量为n=(1,2,1).

　　可取平面PAC的法向量为m=(1,0,0).

　　于是cosm，n===，从而sinm，n=，所以二面角A—PC—D的正弦值为.

　　(3)解：设点E的坐标为(0,0，h)，其中h∈[0,2]，

　　由此得=，又=(2，-1,0)，

　　故cos〈，〉===，所以=cos30°=，解得h=，即AE=.

　　22.(12分)(2014·大纲全国卷)已知抛物线C：y2=2px(p>0)的焦点为F，直线y=4与y轴的交点为P，与C的交点为Q，且|QF|=|PQ|.

　　(1)求C的方程;

　　(2)过F的直线l与C相交于A，B两点，若AB的垂直平分线l′与C相交于M，N两点，且A，M，B，N四点在同一圆上，求l的方程.

　　解：(1)设Q(x0,4)，代入y2=2px得x0=.

　　所以|PQ|=，|QF|=+x0=+.

　　由题设得+=×，解得p=-2(舍去)或p=2.

　　所以C的方程为y2=4x.

　　(2)依题意知l与坐标轴不垂直，故可设l的方程为x=my+1(m≠0).

　　代入y2=4x得y2-4my-4=0.

　　设A(x1，y1)，B(x2，y2)，则y1+y2=4m，y1y2=-4.

　　故AB的中点为D(2m2+1,2m)，

　　|AB|=|y1-y2|=4(m2+1).

　　又l′的斜率为-m，所以l′的方程为x=-y+2m2+3.

　　将上式代入y2=4x，并整理得y2+y-4(2m2+3)=0.

　　设M(x3，y3)，N(x4，y4)，则y3+y4=-，y3y4=-4(2m2+3).

　　故MN的中点为E，

　　|MN|=|y3-y4|=.

　　由于MN垂直平分AB，故A，M，B，N四点在同一圆上等价于|AE|=|BE|=|MN|，从而|AB|2+|DE|2=|MN|2，

　　即4(m2+1)2+2+2

　　=，

　　化简得m2-1=0，解得m=1或m=-1.

　　所求直线l的方程为x-y-1=0或x+y-1=0.