7.以双曲线-=1的中心为顶点，且以该双曲线的右焦点为焦点的抛物线方程是(　　)

　　A.y2=12x B.y2=-12x

　　C.y2=6x D.y2=-6x

　　解析：由-=1，得a2=4，b2=5，∴c2=a2+b2=9.

　　∴右焦点的坐标为(3,0)，故抛物线的焦点坐标为(3,0)，顶点坐标为(0,0).

　　故=3.∴抛物线方程为y2=12x.

　　答案：A

　　8.对于空间任意一点O和不共线的三点A、B、C，有如下关系：

　　6=+2+3，则(　　)

　　A.四点O、A、B、C必共面

　　B.四点P、A、B、C必共面

　　C.四点O、P、B、C必共面

　　D.五点O、P、A、B、C必共面

　　解析：由已知得=++，而++=1，∴四点P、A、B、C共面.

　　答案：B

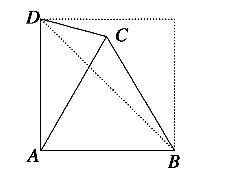
　　9.如图，将边长为1的正方形ABCD沿对角线BD折成直二面角，若点P满足=-+，则||2的值为(　　)

　　A. B.2

　　C. D.

　　解析：由题可知||=1，||=1，||=.〈，〉=45°，〈，〉=45°，〈，〉=60°.

　　∴||2=(-+)2=2+2+2-·+·-·

　　=++2-×1×1×+1××-1××=.

　　答案：D

　　10.已知P是双曲线-=1(a>0，b>0)上的点，F1，F2是其焦点，双曲线的离心率是，且·=0，若△PF1F2的面积为9，则a+b的值为(　　)

　　A.5 B.6

　　C.7 D.8

　　解析：由·=0，得⊥，

　　设||=m，||=n，不妨设m>n，则m2+n2=4c2，m-n=2a，mn=9，=，解得

　　故b=3.因此a+b=7，选C.

　　答案：C

　　11.在正方体ABCD-A1B1C1D1中，直线BC1与平面A1BD所成角的余弦值为(　　)

　　A. B.

　　C. D.

　　解析：建立如下图所示的空间直角坐标系.设正方体的棱长为1，

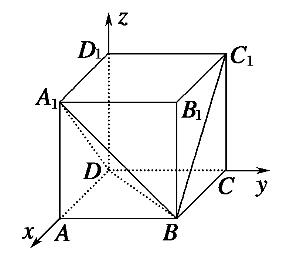
　　则D(0,0,0)，A1(1,0,1)，B(1,1,0)，C1(0,1,1).

　　∴=(1,0,1)，=(1,1,0)，=(-1,0,1).

　　设平面A1BD的法向量为n=(x，y，z)，则n·=0，n·=0.

　　∴令x=1，则n=(1，-1，-1)，

　　∴cos〈n，〉===.

　　∴直线BC1与平面A1BD所成角的正弦值为.

　　∴直线BC1与平面A1BD所成角的余弦值为.

　　答案：C

　　12.双曲线-=1(a>0，b>0)的两个焦点为F1、F2，若P为其上一点，且|PF1|=2|PF2|，则双曲线离心率的取值范围为(　　)

　　A.(1,3) B.(1,3]

　　C.(3，+∞) D.[3，+∞)

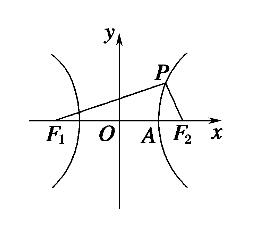
　　解析：由题意知在双曲线上存在一点P，使得|PF1|=2|PF2|，如右图所示.

　　又∵|PF1|-|PF2|=2a，∴|PF2|=2a，

　　即在双曲线右支上恒存在点P使得|PF2|=2a，即|AF2|≤2a.

　　∴|OF2|-|OA|=c-a≤2a.∴c≤3a.

　　又∵c>a，∴a

　　∴1<≤3，即1

　　答案：B