已知函数fx＝xalnxa∈R1当a＝2时求曲线
来源 :中华考试网 2018-01-24
中问答题已知函数f(x)＝x-alnx(a∈R) (1)当a＝2时，求曲线y＝f(x)在点A(1,f(1))处的切线方程； (2)求函数f(x)的极值。
参考答案：
函数f(x)的定义域为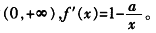
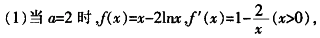因而f(1)＝1,f′(1)＝-1，所以曲线y＝f(x)在点A(1,f(1))处的切线方程为y-1＝-(x-1)，即x+y-2＝0。 
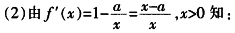①当a≤0时，f′(x)＞0，函数f(x)为(0，+∞)上的增函数，函数f(x)无极值。 ②当a＞0时，由f′(x)＝0，解得x＝a。又当x∈(0，a)时，f′(x)＜0；当x∈(0，+∞)时，f′(x)＞0，从而函数f(x)在x＝a处取得极小值，且极小值为f(a)＝a-alna，无极大值。综上，当a≤0时，函数f(x)无极值；当a＞0时，函数f(x)在x＝a处取得极小值a-alna,无极大值。
