已知|a|=1,|b|=2。 (1)若a∥b,求ab
问答题已知|a|=1,|b|=2。 (1)若a∥b,求ab; (2)若a、b的夹角为60°,求|a+b|; (3)若a-b与a垂直,求当k为何值时,(ka-b)
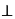
(a+2b)。
参考答案:
(1)ab=±|a||b|=±2。 (2)ab=|a||b|cos60°=1,|a+b|
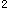
=|a|
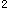
+2ab+|b|
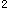
=7,故|a+b|=
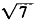
。 (3)若a-b与a垂直,则(a-b)a=0,ab=|a|
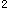
=1,使得(ka-b)
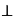
(a+2b),只要(ka-b)(a+2b)=0,即k|a|
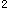
+(2k-1)ab-2|b|
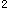
=0,即k+(2k-1)-2×4=0,解得k=3。
查看答案解析 进入焚题库