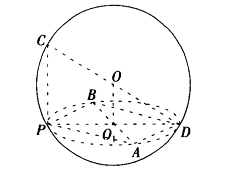
如图,过半径为R的球面上一点P作三条两两垂直的弦
来源 :焚题库 2018-10-22
中问答题
如图,过半径为R的球面上一点P作三条两两垂直的弦PA、PB、PC。
(1)求证:PA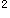 +PB
+PB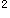 +PC
+PC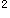 为定值;
为定值;
(2)求三棱锥P-ABC的体积的最大值。
参考答案:
【解析】(1)设过PA、PB的平面截球得 ,由PA⊥PB,则AB是
,由PA⊥PB,则AB是 的直径,连PO
的直径,连PO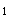 并延长交
并延长交 于D,则PADB是矩形,PD
于D,则PADB是矩形,PD =PA
=PA +PB
+PB 。设O为球心,则OO
。设O为球心,则OO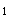 ⊥平面
⊥平面 。由PC⊥
。由PC⊥ 平面,则
平面,则 ∥PC,因此过PC、PD的平面经过球心O,截球得大圆。又PC⊥PD, 则CD是球的直径。故PA
∥PC,因此过PC、PD的平面经过球心O,截球得大圆。又PC⊥PD, 则CD是球的直径。故PA +PB
+PB +PC
+PC =PD
=PD +PC
+PC =CD
=CD =4R
=4R ,为定值。
,为定值。
(2)设PA、PB、PC的长分别为x、y、z,则三棱锥P-ABC的体积 。
。  故
故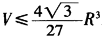 。即
。即 。
。
涉及考点
初中数学考试大纲
第一部分、学科知识
第七章、高中数学学科知识-立体几何

