叙述并证明拉格朗日微分中值定理，并简述拉格朗日
来源 :焚题库 2018-09-11
中问答题【2015年真题】叙述并证明拉格朗日微分中值定理，并简述拉格朗日中值定理与中学数学内容的联系。
参考答案：
如果函数f(x)满足： (1)在闭区间［a，b］上连续； (2)在开区间(a，b)内可导； 则存在ξε(a，b)，使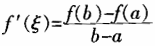
。 证明：已知f(x)在闭区间［a，b］上连续，在开区间(a，b)内可导， 构造辅助函数
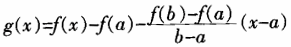验证可得g(a)=g(b)=0 又因为函数g(x)在闭区间［a，b］上连续，在开区间(a，b)内可导，且
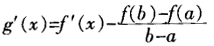根据罗尔定理可知在(a，b)内至少有一点ξ使得g'(ξ)=0 即
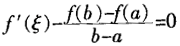由此可得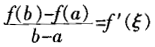
定理证毕。 拉格朗日中值定理在微积分学中是一个重要的理论基础，是应用数学研究函数在区间上整体形态的有力工具。拉格朗日中值定理在中学数学中应用非常广泛，如利用导数来研究函数的某些性质、证明不等式和方程根的存在性、描绘函数的图象、解决极值、最值等等。
