已知是由非负整数组成的无穷数列该数列前n项的最大值记
来源 :焚题库 2018-02-23
中问答题已知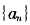 是由非负整数组成的无穷数列,该数列前n项的最大值记为A
是由非负整数组成的无穷数列,该数列前n项的最大值记为A ,第n项之后各项a
,第n项之后各项a +1,a
+1,a +2,…的最小值记为B
+2,…的最小值记为B ,d
,d =A
=A -B
-B 。
(1)若
。
(1)若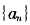 为2,1,4,3,2,1,4,3,…,是一个周期为4的数列(即对任意n∈N
为2,1,4,3,2,1,4,3,…,是一个周期为4的数列(即对任意n∈N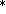 ,a
,a +4=a
+4=a ),写出d
),写出d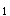 ,d
,d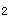 ,d
,d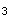 ,d
,d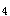 的值;
(2)设d为非负整数,证明:d
的值;
(2)设d为非负整数,证明:d -d(n=1,2,3...)的充分必要条件为
-d(n=1,2,3...)的充分必要条件为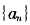 为公差为d的等差数列;
(3)证明:若a
为公差为d的等差数列;
(3)证明:若a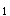 =2,d
=2,d =1(n=1,2,3,…),则
=1(n=1,2,3,…),则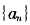 的项只能是1或者2,且有无穷多项为1.
的项只能是1或者2,且有无穷多项为1.
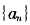 是由非负整数组成的无穷数列,该数列前n项的最大值记为A
是由非负整数组成的无穷数列,该数列前n项的最大值记为A ,第n项之后各项a
,第n项之后各项a +1,a
+1,a +2,…的最小值记为B
+2,…的最小值记为B ,d
,d =A
=A -B
-B 。
(1)若
。
(1)若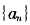 为2,1,4,3,2,1,4,3,…,是一个周期为4的数列(即对任意n∈N
为2,1,4,3,2,1,4,3,…,是一个周期为4的数列(即对任意n∈N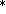 ,a
,a +4=a
+4=a ),写出d
),写出d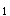 ,d
,d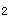 ,d
,d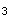 ,d
,d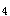 的值;
(2)设d为非负整数,证明:d
的值;
(2)设d为非负整数,证明:d -d(n=1,2,3...)的充分必要条件为
-d(n=1,2,3...)的充分必要条件为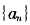 为公差为d的等差数列;
(3)证明:若a
为公差为d的等差数列;
(3)证明:若a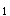 =2,d
=2,d =1(n=1,2,3,…),则
=1(n=1,2,3,…),则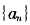 的项只能是1或者2,且有无穷多项为1.
的项只能是1或者2,且有无穷多项为1.参考答案:
(1)d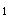 =d
=d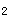 =1,d
=1,d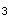 =d
=d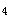 =3;
(2)(充分性)因为
=3;
(2)(充分性)因为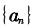 是公差为d的等差数列,且d≥0,所以a
是公差为d的等差数列,且d≥0,所以a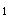 ≤a
≤a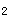 ≤…≤a
≤…≤a ≤…
因此A
≤…
因此A =a
=a ,B
,B =a
=a +1,d
+1,d =a
=a -a
-a +1=-d(n=1,2,3…)d
+1=-d(n=1,2,3…)d =-d(n=1,2,3…)
(必要性)因为d
=-d(n=1,2,3…)
(必要性)因为d =-d≤0(n=1,2,3…),所以A
=-d≤0(n=1,2,3…),所以A =B
=B +d
+d ≤B
≤B 又因为a
又因为a ≤A
≤A ,a
,a +1≥B
+1≥B ,所以a
,所以a ≤a
≤a +1,于是A
+1,于是A =a
=a ,B
,B =a
=a +1。
因此a
+1。
因此a +1-a
+1-a =B
=B -A
-A =-d
=-d =d,即
=d,即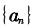 是公差为d的等差数列。
(3)因为a
是公差为d的等差数列。
(3)因为a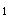 =2,d
=2,d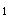 =1,所以A
=1,所以A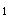 =a
=a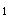 =2,B
=2,B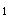 =A
=A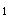 -d
-d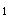 =1。故对任意n≥1,a
=1。故对任意n≥1,a ≥B
≥B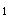 =1。
假设
=1。
假设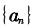 (n≥2)中存在大于2的项。
设m为满足a
(n≥2)中存在大于2的项。
设m为满足a >2的最小正整数,则m≥2,并且对任意1<k<m,a
>2的最小正整数,则m≥2,并且对任意1<k<m,a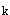 ≤2,
又因为a
≤2,
又因为a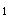 =2,所以A
=2,所以A -1=2,且A
-1=2,且A =a
=a >2。
于是B
>2。
于是B =A
=A -d
-d >1,B
>1,B -1=min{a
-1=min{a ,B
,B }≥2。
故d
}≥2。
故d -1=A
-1=A -1-B
-1-B -1≤0,与d
-1≤0,与d -1=1矛盾。
所以对于任意n≥1,有a
-1=1矛盾。
所以对于任意n≥1,有a ≤2,即非负整数列
≤2,即非负整数列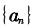 的各项只能为1或2。
因此对任意n≥1,a
的各项只能为1或2。
因此对任意n≥1,a ≤2=a
≤2=a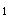 ,所以A
,所以A =2故B
=2故B =A
=A -d
-d =2-1=1。
因此对于任意正整数n,存在m满足m>n,且a
=2-1=1。
因此对于任意正整数n,存在m满足m>n,且a =1,即数列
=1,即数列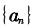 有无穷多项为1。
有无穷多项为1。
