已知椭圆C、抛物线C的焦点均在x轴上
来源 :焚题库 2018-05-08
中问答题已知椭圆C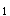 、抛物线C
、抛物线C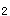 的焦点均在x轴上,C
的焦点均在x轴上,C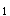 的中心和C
的中心和C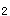 的顶点均为原点O,从每条曲线上取两个点,将其坐标记录于下表中:
的顶点均为原点O,从每条曲线上取两个点,将其坐标记录于下表中:  (1)求C
(1)求C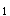 、C
、C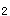 的标准方程: (2)请问是否存在直线L满足条件:①过C
的标准方程: (2)请问是否存在直线L满足条件:①过C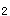 的焦点F;②与C
的焦点F;②与C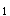 交不同两点M、N,且满足
交不同两点M、N,且满足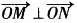 若存在,求出直线L的方程:若不存在,说明理由。
若存在,求出直线L的方程:若不存在,说明理由。
 、抛物线C
、抛物线C 的焦点均在x轴上,C
的焦点均在x轴上,C 的中心和C
的中心和C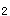 的顶点均为原点O,从每条曲线上取两个点,将其坐标记录于下表中:
的顶点均为原点O,从每条曲线上取两个点,将其坐标记录于下表中:  (1)求C
(1)求C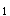 、C
、C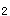 的标准方程: (2)请问是否存在直线L满足条件:①过C
的标准方程: (2)请问是否存在直线L满足条件:①过C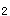 的焦点F;②与C
的焦点F;②与C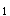 交不同两点M、N,且满足
交不同两点M、N,且满足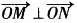 若存在,求出直线L的方程:若不存在,说明理由。
若存在,求出直线L的方程:若不存在,说明理由。参考答案:
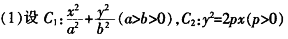 已知的四个点经过分析:(3,2
已知的四个点经过分析:(3,2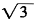 ),(4,-4)在C
),(4,-4)在C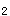 上;(-2,0),
上;(-2,0),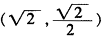 在C
在C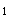 上,分别代入求得p=2,a=2,b=1,则标准方程为:
上,分别代入求得p=2,a=2,b=1,则标准方程为: 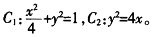 (2)C
(2)C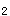 的焦点是(1,0),假设存在这样的直线L且解析式为y=k(x-1),联立C
的焦点是(1,0),假设存在这样的直线L且解析式为y=k(x-1),联立C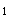 和L的解析式,化简整理得:
和L的解析式,化简整理得: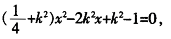 设M(x
设M(x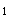 ,y
,y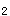 ),N(x
),N(x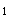 ,y
,y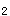 ),由
),由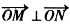 得x
得x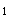 +x
+x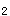 +y
+y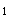 y
y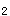 =0① 根据韦达定理有
=0① 根据韦达定理有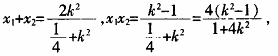
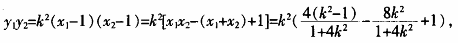
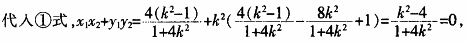 于是有k
于是有k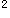 =4,k=±2,因此满足条件的直线存在,L:y=2x-2或y=-2x+2。
=4,k=±2,因此满足条件的直线存在,L:y=2x-2或y=-2x+2。

