问答题已知a>1,设命题p:a(x-2)+1>0,命题q:(x-1)
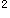
>a(x-2)+1。试寻求使得p、q都是真命题的x的集合。
参考答案:
【解析】设A={x|a(x-2)+1>0},B={x|(x-1)
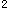
>a(x-2)+1},依题意,求使得p、g都是真命题的x的集合即是求集合A∩B, 因
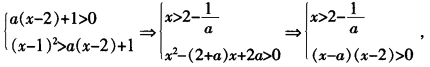
故若1
而
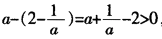
,所以
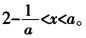
即当1
当a=2时易得使p、q都是真命题的
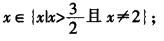
若a>2,则有
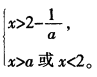
此时使得p、q都是真命题的
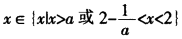
。
查看答案解析 进入焚题库
涉及考点
初中数学考试大纲
第一部分、学科知识
第四章、高中数学学科知识-集合、逻辑与算法