已知R的两组基a=101α=211α=111
来源 :焚题库 2018-09-26
中问答题已知R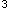 的两组基a
的两组基a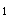 =(1,0,-1)
=(1,0,-1)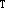 ,α
,α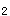 =(2,1,1)
=(2,1,1)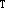 ,α
,α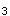 =(1,1,1)
=(1,1,1)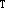 与β
与β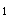 =(0,1,1)
=(0,1,1)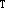 ,β
,β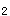 =(-1,1,0)
=(-1,1,0)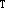 ,β
,β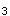 =(1,2,1)
=(1,2,1) (1)求由基α
(1)求由基α ,α
,α ,α
,α 到基β
到基β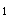 ,β
,β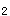 ,β
,β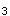 的过渡矩阵; (2)求γ=(9,6,5)
的过渡矩阵; (2)求γ=(9,6,5)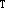 在这两组基下的坐标; (3)求向量δ,使它在这两组基下有相同的坐标。
在这两组基下的坐标; (3)求向量δ,使它在这两组基下有相同的坐标。
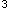 的两组基a
的两组基a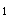 =(1,0,-1)
=(1,0,-1)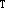 ,α
,α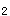 =(2,1,1)
=(2,1,1)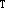 ,α
,α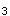 =(1,1,1)
=(1,1,1)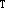 与β
与β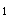 =(0,1,1)
=(0,1,1)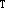 ,β
,β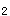 =(-1,1,0)
=(-1,1,0)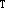 ,β
,β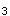 =(1,2,1)
=(1,2,1) (1)求由基α
(1)求由基α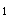 ,α
,α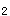 ,α
,α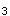 到基β
到基β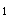 ,β
,β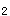 ,β
,β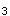 的过渡矩阵; (2)求γ=(9,6,5)
的过渡矩阵; (2)求γ=(9,6,5)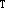 在这两组基下的坐标; (3)求向量δ,使它在这两组基下有相同的坐标。
在这两组基下的坐标; (3)求向量δ,使它在这两组基下有相同的坐标。参考答案:
(1)设从基α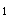 ,α
,α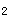 ,α
,α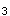 到基β
到基β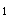 ,β
,β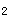 ,β
,β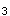 的过渡矩阵是C,则(β
的过渡矩阵是C,则(β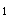 ,β
,β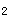 ,β
,β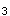 )=(α
)=(α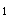 ,α
,α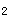 ,α
,α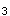 )C,则
)C,则 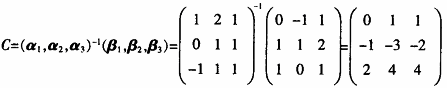 (2)设γ在基β
(2)设γ在基β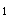 ,β
,β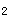 ,β
,β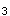 下的坐标是(y
下的坐标是(y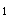 ,y
,y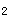 ,y
,y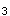 )
)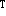 ,即y
,即y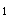 β
β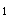 +y
+y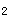 β
β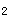 +y
+y β
β =Y,亦即
=Y,亦即 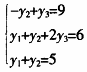 解得:y
解得:y =0,y
=0,y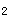 =-4,y
=-4,y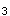 =5 设γ在基α
=5 设γ在基α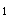 ,α
,α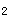 ,α
,α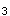 下的坐标是(x
下的坐标是(x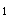 ,x
,x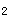 ,x
,x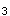 )
) ,按坐标变换公式X=CY,有
,按坐标变换公式X=CY,有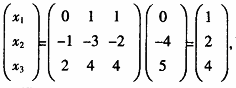 可见γ在这两组基下的坐标分别是(1,2,4)
可见γ在这两组基下的坐标分别是(1,2,4) 和(0,-4,5)
和(0,-4,5) (3)设ξ=x
(3)设ξ=x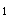 α
α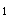 +x
+x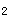 α
α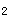 +x
+x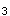 α
α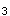 =x
=x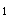 β
β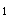 +x
+x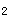 β
β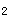 +x
+x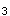 β
β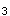 ,即x
,即x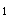 (α
(α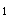 -β
-β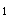 )+x
)+x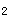 (α
(α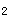 -β
-β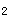 )+x
)+x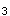 (α
(α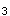 -β
-β )=0
)=0 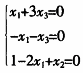 得x
得x =x
=x =x
=x =0 所以,仅有零向量在这两组基下有相同的坐标。
=0 所以,仅有零向量在这两组基下有相同的坐标。

