问答题在平面直角坐标系中,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系。已知点A的极坐标为
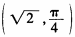
,直线
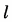
的极坐标方程为
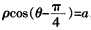
,且点A在直线
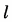
上。 (1)求a的值及直线
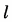
的直角坐标方程; (2)圆C的参数方程为
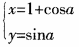
(a为参数),试判断直线
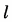
与圆C的位置关系。
参考答案:
(1)由点
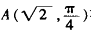
在直线
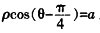
上,可得
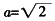
。所以直线的方程可化为ρcosθ+ρsinθ=2,从而直线的直角坐标方程为x+y-2=0。 (2)由已知得圆C的直角坐标方程为(x-1)
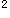
+y
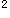
=1,所以圆C的圆心为(1,0),半径r=1,因为圆心C到直线
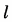
的距离
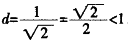
,所以直线
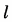
与圆C相交。
查看答案解析 进入焚题库