如下图所示设0＜a＜b函数fx在ab上连续在ab可微
来源 :焚题库 2018-03-29
中问答题【2012年真题】如下图所示，设0＜a＜b，函数f(x)在[a，b]上连续，在(a，b)可微且f(x)＞0，(a)＝f(b)。设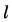
为绕原点O可转动的细棍(射线)，放手后落在函数f(x)的图象上并支撑在点A(ξ，f(ξ))上，从直观上看， 
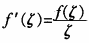。 (*) 证明函数
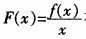在ξ处取得最大值，并由此证明(*)式。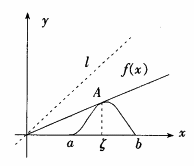 
为绕原点O可转动的细棍(射线)，放手后落在函数f(x)的图象上并支撑在点A(ξ，f(ξ))上，从直观上看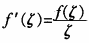， 。 (*) 证明函数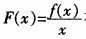在ξ处取得最大值，并由此证明(*)式。 参考答案：
证明：函数f(x)在[a，b]连续，(a，b)可微，b＞a＞0，则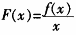
在[a，b]连续，(a，b)可微。F′
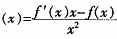，令F′(x)＝0，则F(x)在(a，b)存在极值点满足f′(x)x-f(x)＝0，即为x＝ξ∈(a，b)是函数F(x)的极值点，且
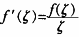。又在(a，b)内，f(a)＝f(b)＝0，且f(x)＞0,则F(a)＝F(b)＝0，且F(ξ)＞F(a)＝F(b)，所以函数
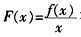在ξ处取得最大值。
