阅读七年级下册"一元一次方程的实践与探索
来源 :焚题库 2018-08-08
中问答题阅读七年级下册"一元一次方程的实践与探索"教学片断,对此案例进行简要评析。 "一元一次方程的实践与探索"教学片段 [多媒体展示] 学校需要制作一块广告牌,请来两名工人。已知师傅单独完成需4天,徒弟单独完成需6天,两人合作需要几天完成?解:设两人合作需要x天完成,根据题意列方程: 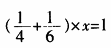 解方程,得x=2.4。答:师徒两人合作需要2.4天完成任务。 [情境拓展] 师:同学们想不想试着提出其他的问题来考考大家呢?如果想,请把问题写下来。教师的话引起了学生们的兴趣,学生个个跃跃欲试、稍后,教师在整理学生们的问题的过程中,发现有的学生按照教科书的提示出了这样一个问题。(1)学校需要制作一块广告牌,请来两名工人。已知师傅单独完成需4天,徒弟单独完成需6天,一人先做一天再和另一人合作,需几天完成?生1:这个问题简单,把一人先做的量从总量中扣掉不就行了。师:你的想法很好!生2(迫切地举手):老师,这道题出错了!问题说"一人先做",可是没说哪个人先做啊。生3:对,可能是师傅先做,也可能是徒弟。所以我们得分两种情况来解决这个问题!师:老师想把这个问题略加改动,还有信心挑战吗?生(齐声):有! [多媒体展示] (2)学校需要制作一块广告牌,请来两名工人。已知师傅单独完成需4天,徒弟单独完成需6天,两人先合作一天再一人单做.几天完成?很快,不少同学积极举手,脸上露出自信的表情。生4:我发现问题(1)是先独做再合作,而问题(2)则正好相反。所以只要将两人合作的工作量扣掉就可以了。生5:跟问题(1)类似,我们也要分两种情况解决。师(露出欣慰的笑容):两位同学的分析太精彩了!看来大家已经感受到了数学中的分类讨论思想。现在老师看看同学们还提出了什么问题。此时学生情绪高涨,期待老师展示下一个题目。 [多媒体展示] (3)学校需要制作一块广告牌,请来两名工人。已知师傅单独完成需4天,徒弟单独完成需6天,两人合作,完成后共得报酬1000元,如果按个人完成的工作量计算报酬,那么该如何分配?生6(按捺不住兴奋):这个问题太简单了,师傅和徒弟的工作效率之比是6:4,所以师傅应得600元,徒弟应得400元。师:你能灵活地应用师徒二人的工作效率之间的关系来解答此题,思维很敏捷呀!师(故作困惑):先由徒弟先做1天,再由两人合作,完成后共得报酬450元。如果按个人完成的工作量计算报酬,那么又该如何分配?学生们认真思考着…… 在问题(3)的启发下,许多学生对本题予以正确解答。
解方程,得x=2.4。答:师徒两人合作需要2.4天完成任务。 [情境拓展] 师:同学们想不想试着提出其他的问题来考考大家呢?如果想,请把问题写下来。教师的话引起了学生们的兴趣,学生个个跃跃欲试、稍后,教师在整理学生们的问题的过程中,发现有的学生按照教科书的提示出了这样一个问题。(1)学校需要制作一块广告牌,请来两名工人。已知师傅单独完成需4天,徒弟单独完成需6天,一人先做一天再和另一人合作,需几天完成?生1:这个问题简单,把一人先做的量从总量中扣掉不就行了。师:你的想法很好!生2(迫切地举手):老师,这道题出错了!问题说"一人先做",可是没说哪个人先做啊。生3:对,可能是师傅先做,也可能是徒弟。所以我们得分两种情况来解决这个问题!师:老师想把这个问题略加改动,还有信心挑战吗?生(齐声):有! [多媒体展示] (2)学校需要制作一块广告牌,请来两名工人。已知师傅单独完成需4天,徒弟单独完成需6天,两人先合作一天再一人单做.几天完成?很快,不少同学积极举手,脸上露出自信的表情。生4:我发现问题(1)是先独做再合作,而问题(2)则正好相反。所以只要将两人合作的工作量扣掉就可以了。生5:跟问题(1)类似,我们也要分两种情况解决。师(露出欣慰的笑容):两位同学的分析太精彩了!看来大家已经感受到了数学中的分类讨论思想。现在老师看看同学们还提出了什么问题。此时学生情绪高涨,期待老师展示下一个题目。 [多媒体展示] (3)学校需要制作一块广告牌,请来两名工人。已知师傅单独完成需4天,徒弟单独完成需6天,两人合作,完成后共得报酬1000元,如果按个人完成的工作量计算报酬,那么该如何分配?生6(按捺不住兴奋):这个问题太简单了,师傅和徒弟的工作效率之比是6:4,所以师傅应得600元,徒弟应得400元。师:你能灵活地应用师徒二人的工作效率之间的关系来解答此题,思维很敏捷呀!师(故作困惑):先由徒弟先做1天,再由两人合作,完成后共得报酬450元。如果按个人完成的工作量计算报酬,那么又该如何分配?学生们认真思考着…… 在问题(3)的启发下,许多学生对本题予以正确解答。
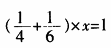 解方程,得x=2.4。答:师徒两人合作需要2.4天完成任务。 [情境拓展] 师:同学们想不想试着提出其他的问题来考考大家呢?如果想,请把问题写下来。教师的话引起了学生们的兴趣,学生个个跃跃欲试、稍后,教师在整理学生们的问题的过程中,发现有的学生按照教科书的提示出了这样一个问题。(1)学校需要制作一块广告牌,请来两名工人。已知师傅单独完成需4天,徒弟单独完成需6天,一人先做一天再和另一人合作,需几天完成?生1:这个问题简单,把一人先做的量从总量中扣掉不就行了。师:你的想法很好!生2(迫切地举手):老师,这道题出错了!问题说"一人先做",可是没说哪个人先做啊。生3:对,可能是师傅先做,也可能是徒弟。所以我们得分两种情况来解决这个问题!师:老师想把这个问题略加改动,还有信心挑战吗?生(齐声):有! [多媒体展示] (2)学校需要制作一块广告牌,请来两名工人。已知师傅单独完成需4天,徒弟单独完成需6天,两人先合作一天再一人单做.几天完成?很快,不少同学积极举手,脸上露出自信的表情。生4:我发现问题(1)是先独做再合作,而问题(2)则正好相反。所以只要将两人合作的工作量扣掉就可以了。生5:跟问题(1)类似,我们也要分两种情况解决。师(露出欣慰的笑容):两位同学的分析太精彩了!看来大家已经感受到了数学中的分类讨论思想。现在老师看看同学们还提出了什么问题。此时学生情绪高涨,期待老师展示下一个题目。 [多媒体展示] (3)学校需要制作一块广告牌,请来两名工人。已知师傅单独完成需4天,徒弟单独完成需6天,两人合作,完成后共得报酬1000元,如果按个人完成的工作量计算报酬,那么该如何分配?生6(按捺不住兴奋):这个问题太简单了,师傅和徒弟的工作效率之比是6:4,所以师傅应得600元,徒弟应得400元。师:你能灵活地应用师徒二人的工作效率之间的关系来解答此题,思维很敏捷呀!师(故作困惑):先由徒弟先做1天,再由两人合作,完成后共得报酬450元。如果按个人完成的工作量计算报酬,那么又该如何分配?学生们认真思考着…… 在问题(3)的启发下,许多学生对本题予以正确解答。
解方程,得x=2.4。答:师徒两人合作需要2.4天完成任务。 [情境拓展] 师:同学们想不想试着提出其他的问题来考考大家呢?如果想,请把问题写下来。教师的话引起了学生们的兴趣,学生个个跃跃欲试、稍后,教师在整理学生们的问题的过程中,发现有的学生按照教科书的提示出了这样一个问题。(1)学校需要制作一块广告牌,请来两名工人。已知师傅单独完成需4天,徒弟单独完成需6天,一人先做一天再和另一人合作,需几天完成?生1:这个问题简单,把一人先做的量从总量中扣掉不就行了。师:你的想法很好!生2(迫切地举手):老师,这道题出错了!问题说"一人先做",可是没说哪个人先做啊。生3:对,可能是师傅先做,也可能是徒弟。所以我们得分两种情况来解决这个问题!师:老师想把这个问题略加改动,还有信心挑战吗?生(齐声):有! [多媒体展示] (2)学校需要制作一块广告牌,请来两名工人。已知师傅单独完成需4天,徒弟单独完成需6天,两人先合作一天再一人单做.几天完成?很快,不少同学积极举手,脸上露出自信的表情。生4:我发现问题(1)是先独做再合作,而问题(2)则正好相反。所以只要将两人合作的工作量扣掉就可以了。生5:跟问题(1)类似,我们也要分两种情况解决。师(露出欣慰的笑容):两位同学的分析太精彩了!看来大家已经感受到了数学中的分类讨论思想。现在老师看看同学们还提出了什么问题。此时学生情绪高涨,期待老师展示下一个题目。 [多媒体展示] (3)学校需要制作一块广告牌,请来两名工人。已知师傅单独完成需4天,徒弟单独完成需6天,两人合作,完成后共得报酬1000元,如果按个人完成的工作量计算报酬,那么该如何分配?生6(按捺不住兴奋):这个问题太简单了,师傅和徒弟的工作效率之比是6:4,所以师傅应得600元,徒弟应得400元。师:你能灵活地应用师徒二人的工作效率之间的关系来解答此题,思维很敏捷呀!师(故作困惑):先由徒弟先做1天,再由两人合作,完成后共得报酬450元。如果按个人完成的工作量计算报酬,那么又该如何分配?学生们认真思考着…… 在问题(3)的启发下,许多学生对本题予以正确解答。参考答案:
【参考答案】"工程问题"虽然在小学就涉及到了,但仍然是七年级学生难以掌握的问题。这个教学片段以"工程问题"中的基本例题为"根基",教师有目的、有意识地筛选出学生们自己提出的问题进行解决:从"两人合作"到"一人先做再合作"到"先合作再一人单做"再到"报酬的合理分配"。这四个问题,采用"给出情境,让学生参与"的教学方法,对教科书中的例题进行了合理的变形、转化、拓展与综合,深入挖掘其中潜在的数学思想方法,并揭示其丰富内涵。不但有利于学生掌握基础知识、激发学生的学习兴趣、发挥学生的想象力和创造精神,而且对培养学生的应变能力、开拓思维,提高学生对数学建模思想的认识等都是很有益的。这种训练,也符合目前中考命题"源于教科书、高于教科书"的原则,与素质教育要求的"培养学生的创新能力"相吻合。由此看到,教科书仅仅只是提供了最基本的资源,并不是唯一的资源,教师作为学生学习的组织者和指导者,应该在钻研课程标准、教科书和学生情况的过程中,找准这三者之间的联系,并在数学教学中,正确理解教科书编者的意图,从实际出发,从学生的知识水平和学习内容以及学生的情绪出发。教师应对教科书蓝本进行"改编",把封闭式问题变为开放式、探究式问题,并增加学生探索的梯度,培养学生大胆发现问题、解决问题的能力;还应对教科书进行"拓展",使问题延伸,增加学生探索问题的广度和深度,引导学生对知识进行再发现、再创造,体现教学的实效性。涉及考点
初中数学考试大纲
第四部分、教学技能
第二章、教学实施

