已知四棱锥P-ABCD,它的底面是边长为a的菱形
来源 :焚题库 2018-06-13
中问答题
已知四棱锥P-ABCD,它的底面是边长为a的菱形，且∠ABC=120°，PC⊥平面ABCD，又PC=a，E为PA的中点。
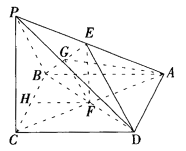
（1）求证：平面EBD⊥平面ABCD;
（2）求点E到平面PBC的距离；
（3）求二面角A-BE-D的大小。
参考答案：
【解析】（1）在四棱锥P-ABCD中，底面是菱形，连结AC、BD，交于F，则F为AC的中点。又E为PA的中点、则EF∥PC。又由PC⊥平面ABCD，则EF⊥平面ABCD，又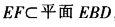
，故平面EBD⊥平面ABCD。
（2）由EF∥PC，则EF∥平面PBC，故E到平面PBC的距离是EF到平面PBC的距离。过F作FH⊥BC交BC于H，由PC⊥平面ABCD，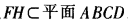
，则PC⊥FH。又BC⊥FH，则FH⊥_平面PBC，则FH是F到平面PBC的距离，也是E到平面PBC的距离。由∠FCH=30°，
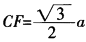。故
。
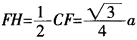（3）取BE的中点G，连接FG、AG，由（1）的结论，平面BDE⊥平面ABCD，AF⊥BD，则AF⊥平面BDE。由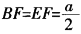
，则FG⊥BE，由三垂线定理得，AG⊥BE，故∠FGA为二面角D-BE-A的平面角。 
，
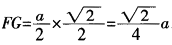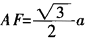。故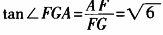
，
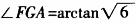，即二面角A-BE-D的大小为
。
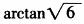涉及考点
初中数学考试大纲
第一部分、学科知识
第七章、高中数学学科知识-立体几何
