问答题已知函数
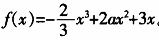
(1)当a=
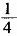
时,求函数f(x)在[-2,2]上的最大值、最小值; (2)令g(x)=ln(1+x)+3-f′(x),若g(x)在
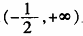
上单调递增,求实数a的取值范围。
参考答案:
(1)f′(x)=-2x
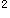
+4ax+3,当a=
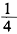
时f′(x)=-2x
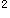
+x+3=(-2x+3)(x+1),令f′(x)=0得x
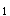
=
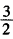
,x
=-1,当x变化时f′(x)和f(x)的变化情况如下表:

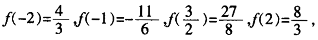

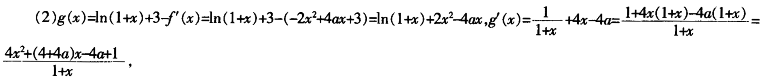
由题目知在(-
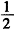
,+∞)上g′(x)>0恒成立,等价于二次函数h(x)=4x
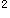
+(4-4a)x-4a+1在(-
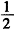
,+∞)上恒大于0,根据二次函数的性质有:
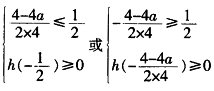
解之得a≤0。
查看答案解析 进入焚题库