设三维空间中椭圆
来源 :焚题库 2018-05-09
中问答题【2014年真题】设三维空间中椭圆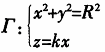 (1)证明
(1)证明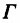 的中心为原点,并求
的中心为原点,并求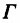 的长轴和短轴的长度。 (2)证明:任给一个椭圆,存在参数R和k,使得
的长轴和短轴的长度。 (2)证明:任给一个椭圆,存在参数R和k,使得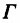 与给定椭圆全等。
与给定椭圆全等。
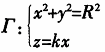 (1)证明
(1)证明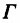 的中心为原点,并求
的中心为原点,并求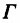 的长轴和短轴的长度。 (2)证明:任给一个椭圆,存在参数R和k,使得
的长轴和短轴的长度。 (2)证明:任给一个椭圆,存在参数R和k,使得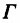 与给定椭圆全等。
与给定椭圆全等。参考答案:
证明:(1)由已知得,椭圆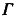 为圆柱x
为圆柱x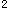 +y
+y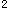 =R
=R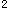 与z=kx平面相截所得,因为圆柱x
与z=kx平面相截所得,因为圆柱x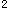 +y
+y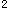 =R
=R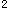 与的中心为原点,z=kx平面的中心为原点。故的中心为原点。椭圆
与的中心为原点,z=kx平面的中心为原点。故的中心为原点。椭圆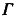 与直线
与直线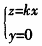 的交点为椭圆的两个端点(R,0,kR),(-R,0,-kR),因为椭圆的长轴与短轴相互垂直,则另两个端点为椭圆与直线
的交点为椭圆的两个端点(R,0,kR),(-R,0,-kR),因为椭圆的长轴与短轴相互垂直,则另两个端点为椭圆与直线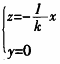 的交点
的交点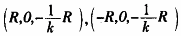 。当|k|≥1时长轴长为
。当|k|≥1时长轴长为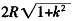 ,短轴长为
,短轴长为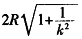 ,当|k|<1时长轴长为
,当|k|<1时长轴长为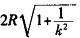 ,短轴长为
,短轴长为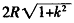 。 (2)在平面z=kx上以直线
。 (2)在平面z=kx上以直线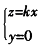 为横轴m,以直线
为横轴m,以直线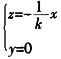 为纵轴n建立直角坐标系,可得
为纵轴n建立直角坐标系,可得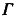 的平面方程为
的平面方程为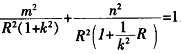 。其中长短轴之比
。其中长短轴之比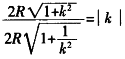 与R无关,故对任意给定的一个椭圆其两轴长分别为a,b均可找到参数k,R使得a
与R无关,故对任意给定的一个椭圆其两轴长分别为a,b均可找到参数k,R使得a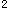 =R
=R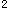 (1+k
(1+k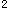 ),
),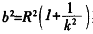 其中
其中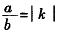 。即证。
。即证。

