已知p:方程x+mx+1=0有两个不等负实根
来源 :焚题库 2018-07-27
中问答题已知p:方程x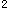
+mx+1=0有两个不等负实根。q：方程4x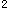+4（m-2）x+1=0无实根。若p或q为真，p且q为假。求实数m的取值范围。
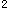+mx+1=0有两个不等负实根。q：方程4x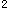+4（m-2）x+1=0无实根。若p或q为真，p且q为假。求实数m的取值范围。参考答案：
【解析】因为p或q为真,p且q为假，则必然p与q中有一真一假。分两种情况：p为真，q为假；q为真，p为假。（1）若p为真，则q为假。 p为真，方程x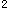
+mx+1=0有两个不等负实根成立，即△=m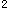-4>0，x
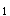+x
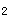=-m<0，解得：m>2或m<-2，m>0。综上两式得到：m>2。 q为假，方程4x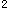+4（m-2）x+1=0无实根不成立，即有实数根，△=16（m-2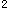）-16≥0，所以m≥3或m≤1。取交集得到，m≥3；（2）若q为真，则p为假。 q为真，即方程4x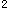+4（m-2）x+1=0无实根成立，即△=16（m-2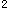）-16<0，所以1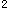-4≤0，或②有两个不等正实根，△=m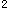-4>0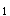，x+x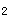=-m>0。解得，①-2≤m≤2或②m<-2，所以m≤2。取交集得到：1涉及考点
初中数学考试大纲
第一部分、学科知识
第四章、高中数学学科知识-集合、逻辑与算法
