2017年甘肃天水一中2014级第一学期第二次考试
来源 :中华考试网 2016-12-05
中参考答案:
选择题
BCCAD DBCAB DC
填空题
13. 2 14. 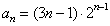 15. 1030 16.②③
15. 1030 16.②③
三、解答题
17.(1)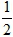 ;(2)
;(2)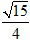 。
。
18.(1)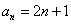 ;(2)
;(2)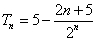 .
.
19.(1)证明 连接AC,AC交BD于O,连接EO.
∵底面ABCD是正方形,∴点O是AC的中点.在△PAC中,EO是中位线,∴PA∥EO.
而EO?平面EDB且PA?平面EDB, ∴PA∥平面EDB.
2)证明 ∵PD⊥底面ABCD,且DC?底面ABCD,
∴PD⊥DC.∵PD=DC,可知△PDC是等腰直角三角形.
而DE是斜边PC的中线,∴DE⊥PC.①
同样,由PD⊥底面ABCD,BC?平面ABCD, 得PD⊥BC.
∵底面ABCD是正方形,有DC⊥BC.又PD∩CD=D,∴BC⊥平面PDC.
而DE?平面PDC,∴BC⊥DE.②由①和②且PC∩BC=C可推得DE⊥平面PBC.
而PB?平面PBC,∴DE⊥PB.又EF⊥PB且DE∩EF=E, ∴PB⊥平面EFD.
3)解 由(2)知,PB⊥DF. 故∠EFD是二面角C-PB-D的平面角.
由(2)知DE⊥EF,PD⊥DB. 设正方形ABCD的边长为a,则PD=DC=a,BD=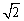 a,
a,
PB=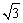 a,PC=
a,PC=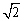 a,DE=
a,DE=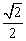 a,在Rt△PDB中,DF=
a,在Rt△PDB中,DF=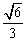 a.
a.
在Rt△EFD中,sin∠EFD=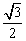 ,∴∠EFD=60°. ∴二面角C-PB-D的大小为60°.
,∴∠EFD=60°. ∴二面角C-PB-D的大小为60°.
20.(1)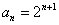 ,
,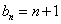 ;(2)
;(2)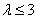 .
.
(2)∵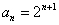 ,∴
,∴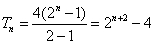 .
.
不等式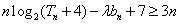 化为
化为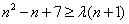 ,∵
,∵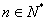 ,
,
∴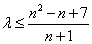 对一切
对一切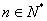 恒成立.
恒成立.
 而
而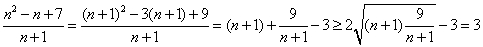 ,
,
 当且仅当
当且仅当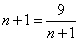 即
即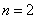 时等号成立,∴
时等号成立,∴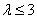
21.(1)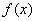 的定义域为
的定义域为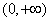 ,
,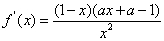
当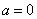 时,由
时,由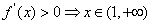 ,∴
,∴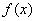 的单调增区间为
的单调增区间为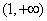
由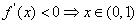 ,∴
,∴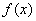 的单调减区间为
的单调减区间为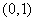 ,
,
当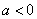 时,由
时,由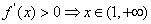 ,∴
,∴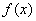 的单调增区间为
的单调增区间为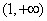 ,
,
由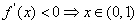 ,∴
,∴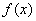 的单调减区间为
的单调减区间为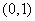 ,
,
当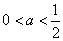 时,由
时,由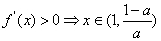 ,∴
,∴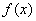 的单调增区间为
的单调增区间为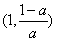 ,
,
由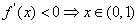 和
和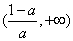 ,∴
,∴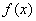 的单调减区间为
的单调减区间为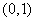 和
和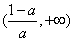 .
.
当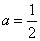 时,
时,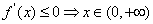 ,∴
,∴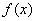 的单调减区间为
的单调减区间为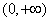 ,
,
.综上所述当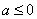 时,
时,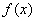 的单调增区间为
的单调增区间为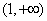 ,单调减区间为
,单调减区间为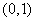 .
.
当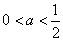 时,
时,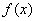 的单调增区间为
的单调增区间为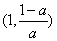 ,单调减区间为
,单调减区间为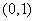 和
和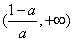 ,
,
当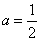 时,
时,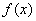 的单调减区间为
的单调减区间为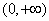 .
.
(2)用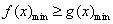 ,而
,而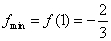 ,对
,对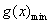 分三种情况:
分三种情况:
①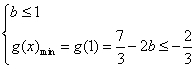
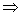 无解;
无解;
②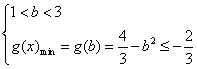
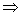
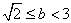 ;
;
③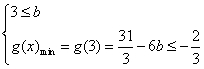
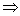
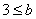 .
.
综上:∴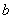 的取值范围为
的取值范围为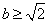 .
.
22.(1) 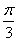 ,(x-
,(x-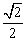 )2+(y-
)2+(y-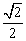 )2=1 (2)
)2=1 (2) 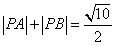
23.( Ⅰ)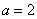 (Ⅱ)
(Ⅱ)