1.某高校根据随机抽取 1000 名学生的调查数据推断得出，95%的置信度下学生每月生活费平均支出的置信区间为 1000-1500 元。这表明该校有 95%的学生每月生活费的平均支出在 1000-1500 元之间。

A、对

B、错

参考答案: B

题目解析:在95%的置信度下学生每月生活费平均支出的置信区间为[1000，1500]。

2.下列表述中正确的有( )。

A、总体均值的置信区间都是由样本均值加减估计误差得到

B、在小样本情况下，对总体均值的估计都是建立在总体服从正态分布的假定条件下

C、当样本量n充分大时，样本均值的分布近似服从正态分布

D、当总体服从正态分布时，无论样本量大小，样本均值一定服从正态分布

E、对总体均值进行区间估计时，不需要考虑总体方差是否已知

参考答案: A,B,D

题目解析:选项C错误，若总体为未知的非正态总体，当样本量n充分大时，样本均值的分布近似服从正态分布;选项E错误，对总体均值进行区间估计时，需要考虑总体方差是否已知，当总体方差未知时，需要用样本方差来代替总体方差。

3.今从某地区抽取 1000 户居民家庭调查其每月的平均生活费用。按照当地贫困划分标准，其中有 100 户为贫困户，则贫困率 95%的置信区间为( )。(注：Z 0.025 = 1.96 )

A、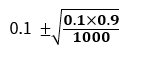

B、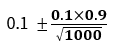

C、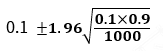

D、

参考答案: C

4.从100个住户中随机抽取了10户，调查其月消费支出额。经计算得到10户的平均月消费支出额为3500元，标准差为300元。假定总体服从正态分布，则总体平均月消费支出额95%的置信区间为：( )。

A、正确

B、错误

参考答案: B

题目解析:在小样本(n<30)的情况下，如果总体的方差未知，样本均值经过标准化后服从自由度为n -1的t分布。在1-α的置信度下，总体均值的置信区间为：

即

5.在大样本条件下，根据中心极限定理，如果( )，则二项分布可用正态分布近似。

A、np≤5，n(1-p)≤5

B、np≥5，n(1-p)≥5

C、np≥5，n(1-p)≤5

D、np≤5，n(1-p)≥5

参考答案: B

题目解析:在大样本条件下，根据中心极限定理，若np≥5，n (1-p)≥5，则二项分布可用正态分布近似。

6.随着样本容量的增大，点估计量的值越来越接近被估计总体参数的真实值，这种性质是估计量的()

A、无偏性

B、稳健性

C、有效性

D、一致性

参考答案: D

题目解析:点估计的评估标准有以下三个：①无偏性，是指估计量抽样分布的期望值等于被估计的总体参数;②有效性，是指估计量的方差尽可能小;③一致性，是指随着样本量的增大，点估计量的值越来越接近被估计总体的参数。

7.抽样估计的有效性，是指作为优良估计量的方差，应该比其他估计量的方差( )。

A、大

B、小

C、相等

D、无关

参考答案: B

题目解析:有效性是指估计量的方差尽可能小。一个无偏的估计量并不意味着它就非常接近被估计的总体参数，估计量与参数的接近程度使用估计量的方差来度量的。对同一个总体参数的两个无偏估计量，有更小方差的估计量更有效。

8.下列表述中，错误的是( )。

A、总体均值的置信区间都是由样本均值加减估计误差得到

B、在小样本情况下，对总体均值的估计都是建立在总体服从正态分布的假定条件下

C、当样本量n充分大时，样本均值的分布近似服从正态分布

D、当总体服从正态分布时，样本均值不服从正态分布

E、对总体均值进行区间估计时，不需要考虑总体方差是否已知

参考答案: D,E

题目解析:当总体服从正态分布时，样本均值也服从正态分布。对总体均值进行区间估计时，需要分两种情况：方差已知和方差未知。

9.总体方差的无偏估计量是( )。

A、

B、

C、

D、

参考答案: B