第五章 相关分析与回归分析

　　(一) 相关分析

　　相关分析的主要内容包括：

　　一是确定现象之间有无关系，这是相关分析的起点，只有存在相互储存关系，才有必要进行进一步的分析。

　　二是确定相关关系的表现形式，只有判明了现象之间相关关系的具体表现形式，才能运用相应的回归分析方法进一步分析现象之间的数量依存关系，如果把曲线相关误认为是直线相关，按直线相关来分析，便会出现认识上的偏差，导致错误的结论。

　　三是测定相关关系的密切程度。

　　散点图又称相关图。

　　相关的形态：

　　若变量Y与变量X的相关关系表现为线性组合，或绘制的散点图近似地表现为一条直线或直线带，则称之为线性相关，若Y与X是非线性组合，或绘制的散点图近似地表现为一条曲线，则称之为非线性相关或曲线相关。

　　相关的方向：

　　当两个变量的变动方向总体上相同，即一个变量增加，另一个变量也相应地增加，或一个变量减少，另一个变量也相应地减少时，两个变量之间的关系属于正相关;若两个变量变动的方向总体上相反，即一个变量增加的同时，另一个变量随之减少时，两个变量之间的关系属于负相关。

　　相关系数是测定变量之间关系密切程度的量，它能够以数字准确地描述变量之间的相关程度。相关系数的计算公式是：

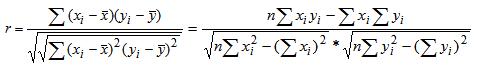
　　相关系数具有如下性质：

　　1.r的取值范围在-1~1，即-1≤r≤1.r>0表明x与y之间存在正线性相关关系;r<0表明x与y之间存在负线性相关关系;r值越接近1(或-1)就越正(或负)相关，越接近0，就越不相关。r=1或r=-1表明x与y是安全相关关系(实际上就是函数关系)。

　　2.r具有对称性。

　　3.r数值大小与X和y的数据原点及计量尺度无关。

　　4.r仅仅是X与y之间线性关系的一个度量，它不能用于描述非线性关系。这意味着，r=0只表示两个变量之间不存在线性相关，并不表明变量之间没有任何关系，比如他们之间可能存在非线性相关关系。

　　5.r虽然是两个变量之间线性关系的一个度量，却不一定意味着x与y一定有因果关系。

　　可将相关程度分为以下几种情况:

　　当|r|≥0.8时，可视为高度相关;当0.5≤|r|<0.8时，可视为中度相关;当0.3≤|r|<0.5时，可视为低度相关;当|r|<0.3时，说明两个变量之间的相关程度极弱。

　　相关系数的检验：

　　相关系数的检验通常用t分布检验，该检验可以用于小样本，也可以用于大样本。检验的具体步骤如下：

　　首先确定原假设：

　　H0:两变量之间不存在线线性相关 或 H0:p=0

　　H1:两变量之间存在线线性相关 或 H1:p≠0

　　其次，计算统计量t值

　　t=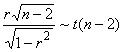

　　最后，利用其对应的概率值进行判断，如果概率值小于或等于指定的显著性水平(一般α=0.05)，则我们可以拒绝原假设，接受备择假设，即两变量之间存在线性相关关系。否则不能原假设，可以认为两变量之间不存在显著的相关关系。

　　(二) 一元性回归分析

　　回归分析的主要内容有以下几个方面：

　　一是从样本数据出发，确定变量之间的数学关系式;

　　二是估计回归模型参数;

　　三是对所确定的关系式进行各种统计检验，并从影响某一特定变量的诸多变量中找出影响显著的变量。

　　线性理论回归模型为：y=β0+β1X+ε—y为因变量，x为自变量，βi为未知参数，其中β0为回归常数，β1为回归系数。ε为随机误差项。