函数f(x)=x2+bx+c的图像经过点(-1,0),(3,0),则f(x)的最小值为
简答题 【2020年真题】函数f(x)=x2+bx+c的图像经过点(-1,0),(3,0),则f(x)的最小值为______。
参考答案:-4
答案解析:本题主要考查的知识点为一元二次函数的性质。由于函数开口向上,故其在对称轴处取得最小值,又函数过点(-1,0),(3,0),故其对称轴为x=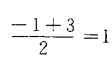 ,
,
fmin(1)=1+b+c,而f(-1)=1-b+c=0,f(3)=9+3b+c=0,得b=-2,c=-3,故fmin(1)=1-2-3=-4。
登录查看解析 进入题库练习