简答题 试利用结构的对称性用位移法计算图(a)所示刚架，并绘出最后弯矩图。

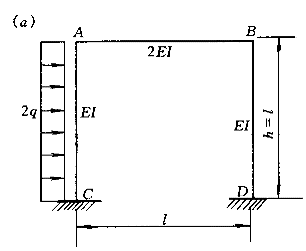
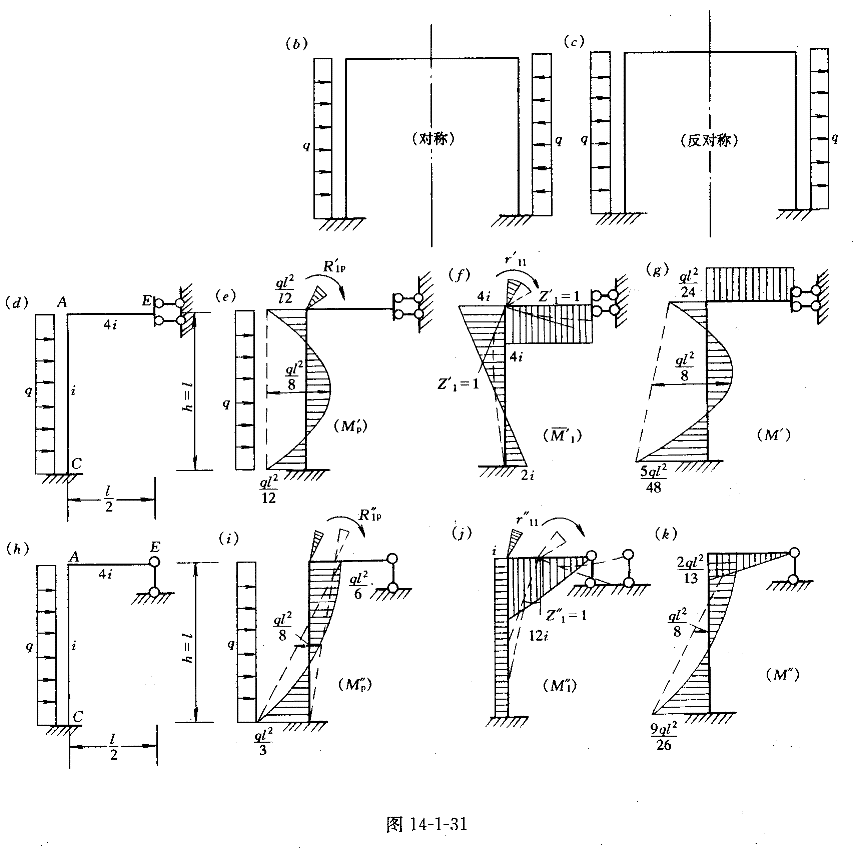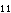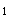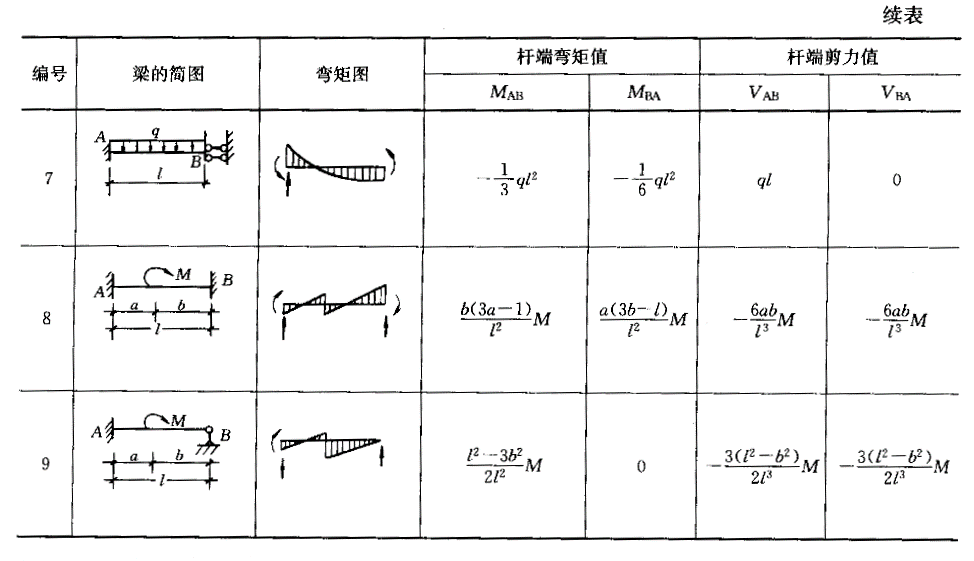
参考答案： 结构所受的荷载是不对称的，可将其分解为对称的和反对称的，如图14-1-31b和c所示。现就对称的和反对称的分别计算如下： 1)在对称荷载作用下的计算(图14-1-31b)在对称荷载作用下，处于对称轴上的横梁中点截面，无角位移和水平线位移，同时剪力等于零；处于对称轴两侧位置对称的节点A和节点B，其角位移等值而反向（对称），即φ=-φ。因此，可以取出半边刚架来计算，一半刚架对另一半刚架所起的约束作用可以模拟成沿竖直方向可移动的定向支座，如图14-1-31d所示。此时，刚架只有一个刚节点A，而且无线位移，故只有一个角位移未知量。基本结构是在刚节点A上加上附加刚臂约束，相应的位移法典型方程是 r′Z′+R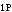′=0 由荷载和单位位移所产生的弯矩图，可查表14-1-1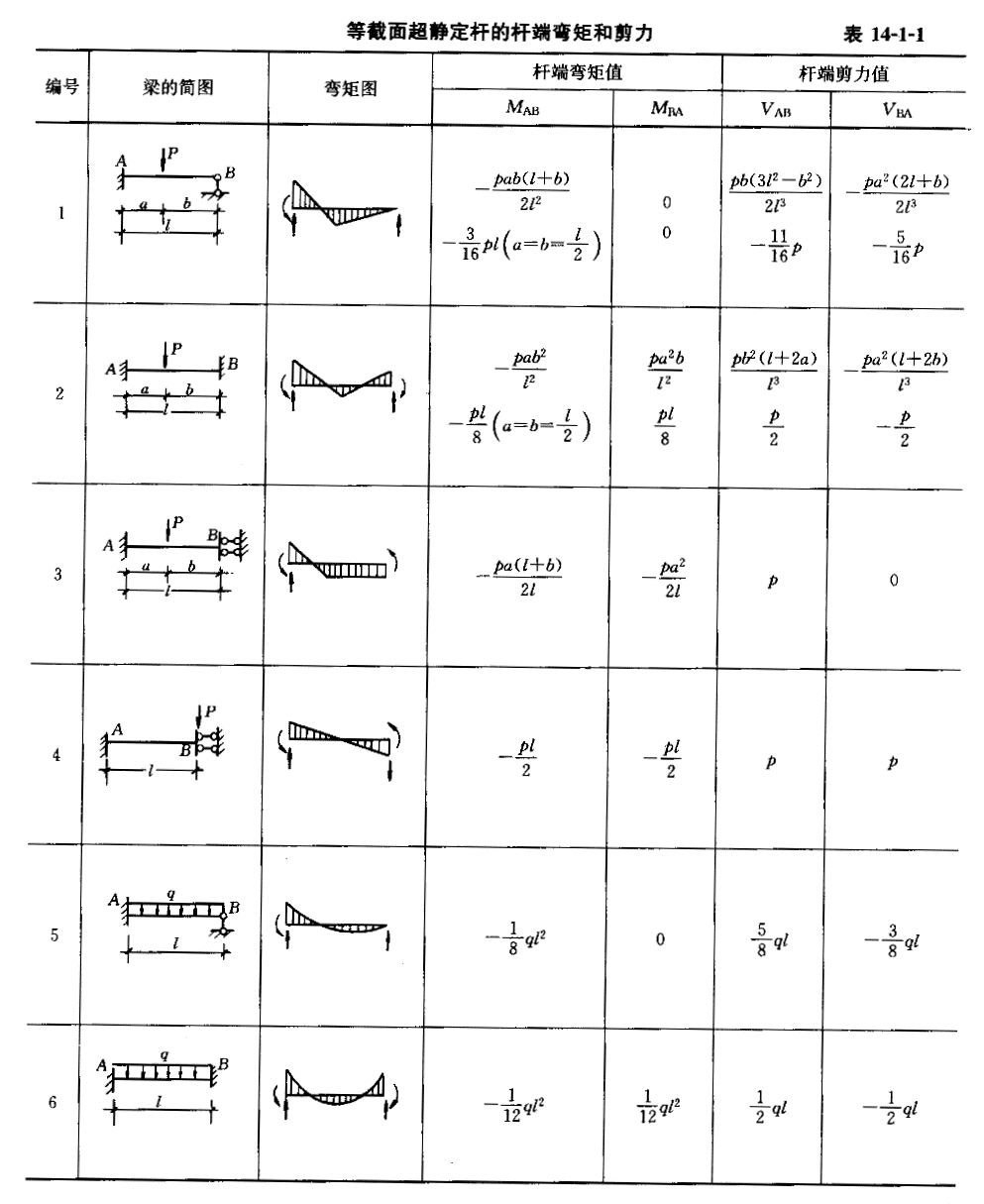 和14-1-2 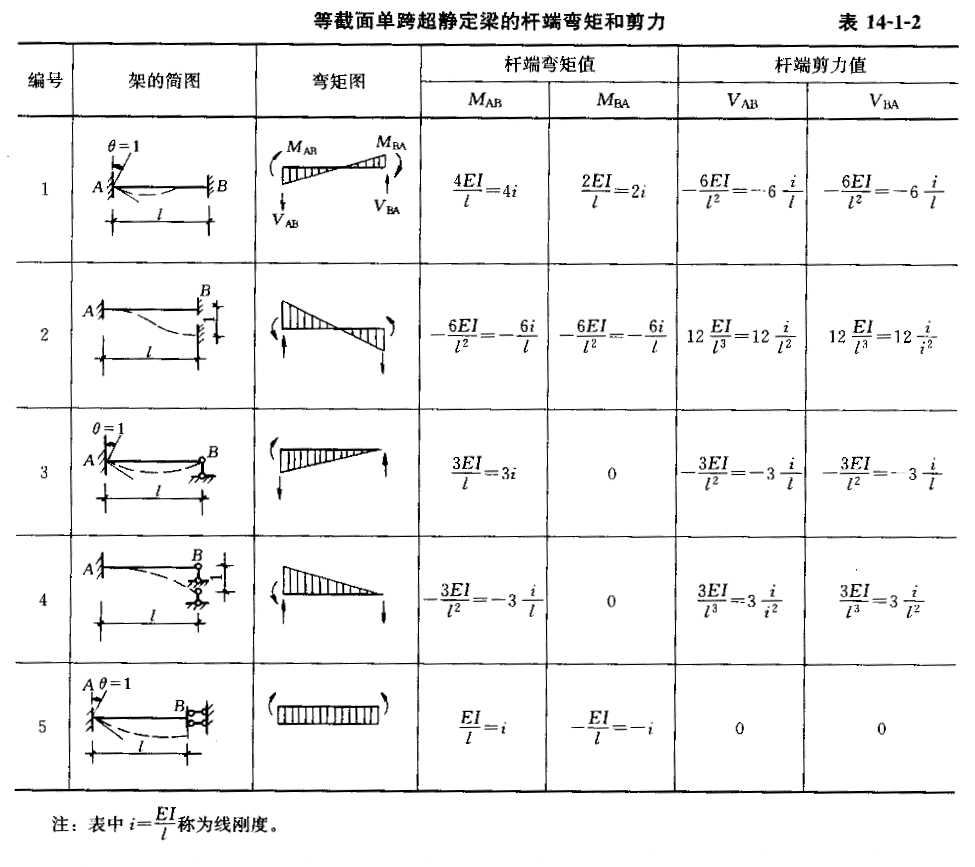求得，故得荷载弯矩图和单位弯矩图，如图14-1-31e和f所示。根据节点的力矩平衡条件，求得 r′=4i+i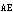=4i+4i=8i 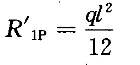注意：此时横梁AE的线刚度为 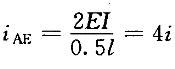将求得的系数和自由项，代入位移法典型方程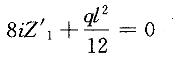，得 由此解得 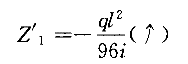这样，按照叠加原理，由式 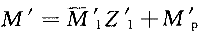便可作出在对称荷载作用下左半刚架的弯矩图，如图14-1-31g所示。此时，右半刚架的弯矩图，可根据对称条件作出。 2)在反对称荷载作用下的计算(图14-1-31c)在反对称荷载作用下，处于对称轴上的横梁中点截面，无竖向线位移，同时弯矩和轴力都等于零；处于对称轴两侧位置对称的刚节点A和刚节点B，其角位移等值同向（反对称），即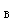φ=φ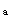。因此，也可取出半边刚架来计算，一半刚架对另一半刚架所起的约束作用，可以将其模拟成既可转动又可沿水平方向移动的竖向活动铰支座，如图14-1-31h所示。此时，刚架也只有一个刚接节点A，有一个角位移。同时，刚接节点A还可沿水平方向移动，有一个线位移，按道理还应该有一个线位移未知量。但是，由于柱内的剪力是可以根据平衡条件确定的，在这种情况下，亦可不把柱端的水平位移当作位移未知量，而把柱子看成是两端节点在垂直于杆轴方向可以作相对移动的，即下端固定、上端为定向支座的单跨超静定梁。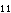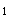因此，也只有一个角位移未知数，相应的位移法典型方程为r″Z″+R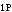″=0由荷载产生的弯矩图，可查表14-1-1 求得，（横梁AE因无横向荷载，故弯矩为零）如图14-1-31i所示，由单位位移产生的弯矩图，可查表14-1-2求得如图14-1-31j所示。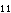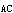根据节点的力矩平衡条件，求得 r″=i+3i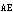=i+3·4i=13i 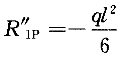将求得的系数和自由项，代入位移法典型方程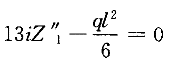，得 由此解得 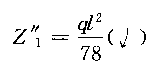这样，按照叠加原理，由式 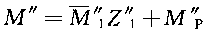便可作出在反对称荷载作用下左半刚架的弯矩图，如图14-1-31k所示。此时，右半刚架的弯矩图，可根据反对称条件作出。最后，将对称荷载作用下所产生的弯矩图和反对称荷载作用下所产生的弯矩图进行叠加，即得刚架在原非对称荷载作用下所产生的弯矩图，如图14-1-32所示。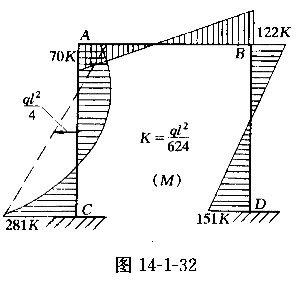

登录查看解析 进入题库练习

答案解析:无

相关知识：十四、结构力学与结构设计