与圆x2+y2=4关于点M(3,2)成中心对称的曲线方程
单项选择题 与圆x2+y2=4关于点M(3,2)成中心对称的曲线方程是( )
A.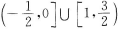
B.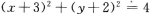
C.
D.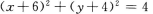
正确答案:C
答案解析:
与圆关于点M成中心对称的曲线还是圆.只要求出圆心和半径,即可求出圆的方程.圆x2+y2=4的圆心(0,0)关于点M(3,2)成中心对称的点为(6,4),所以所求圆的圆心为(6,4),半径与对称圆的半径相等,所以所求圆的方程为(x-6)2+(y-4)2=4.
【考点指要】本题主要考查中心对称图形的定义、中点坐标公式的灵活运用、圆的标准方程的求法,这些主要概念在考试大纲中要求掌握,同时也是近几年经常考到的知识点.
登录查看解析 进入题库练习