已知关于x,y的方程x2+y2+4xsinθ+ 4xsinθ – 4ycosθ=0
简答题 【2017年真题】已知关于x,y的方程 x
2 + y
2 + 4xsinθ – 4ycosθ=0
(1)证明:无论θ为何值,方程均表示半径为定长的圆;
(2)当
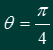
时,判断该圆与直线y=x的位置关系.
参考答案:证明:
化简原方程得: X2 + 4xsinθ + 4sin2θ + y2 - 4ycosθ + 4cos2θ - 4sin2θ - 4cos2θ = 0,(x+2sinθ)2 +(y-2cosθ)2 = 4,所以,无论 θ为何值,方程均表示半径为2的圆.

答案解析:
登录查看解析 进入题库练习