2022年考研《数学一》辅导试题及答案2
来源 :中华考试网 2021-04-24
中 [单选题]设![]() 是某二阶常系数非齐次线性微分方程的解,则该方程的通解是()。
是某二阶常系数非齐次线性微分方程的解,则该方程的通解是()。
A![]()
B![]()
C![]()
参考答案:A
[问答题]设连续函数f(x)非负,且![]() ,则在区间[0,2]上的平均值为______。
,则在区间[0,2]上的平均值为______。
参考答案:2
[问答题]已知向量组A:α1=(0,1,2,3)T,α2=(3,0,1,2)T,α3=(2,3,0,1)T;B:β1=(2,1,1,2)T,β2=(0,-2,1,1)T,β3=(4,4,1,3)T。试证B组能由A组线性表示,但A组不能由B组线性表示。
参考答案:

[问答题]已知3阶矩阵A的第一行是(a,b,c),a,b,c不全为零矩阵B=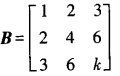 (k为常数),且AB=O求线性方程组Ax=0的通解。
(k为常数),且AB=O求线性方程组Ax=0的通解。
参考答案:由于AB=O,故r(A)+r(B)≤3,又由a,b,c不全为零,可知r(A)≥1。
当k≠9时,r(B)=2,于是r(A)=1;
当k=9时,r(B)=1,于是r(A)=1或r(A)=2。
对于k≠9,由AB=O可得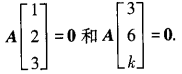
由于η1=(1,2,3)T,η2=(3,6,k)T线性无关。故η1,η2为Ax=0的一个基础解系,于是Ax=0的通解为
x=c1η1+c2η2,其中c1,c2为任意常数。
对于k=9,分别就r(A)=2和r(A)=1进行讨论。
如果r(A)=2,则Ax=0的基础解系由一个向量构成。又因为 ,所以Ax=0的通解为x=c3(1,2,3)T,其中c3为任意常数。
,所以Ax=0的通解为x=c3(1,2,3)T,其中c3为任意常数。
如果r(A)=1,则Ax=0的基础解系由两个线性无关的解向量构成。又因为A的第一行为(a,b,c)且a,b,c不全为零,所以Ax=0等价于ax1+bx2+x3=0,不妨设a≠0,η3=(-b,a,0)T,η4=(-c,0,a)T是Ax=0的两个线性无关的解,故Ax=0的通解为
x=c4η3+c5η4,其中c4,c5为任意常数。
[问答题]设某种元件的使用寿命X的概率密度为: 其中θ>0为未知参数X1,X2,…,Xn为来自总体X的简单随机样本,求θ的最大似然估计量
其中θ>0为未知参数X1,X2,…,Xn为来自总体X的简单随机样本,求θ的最大似然估计量![]() ,并讨论无偏性。 参考答案:设样本值为X1,X2,…,Xn,则似然函数为:
,并讨论无偏性。 参考答案:设样本值为X1,X2,…,Xn,则似然函数为:

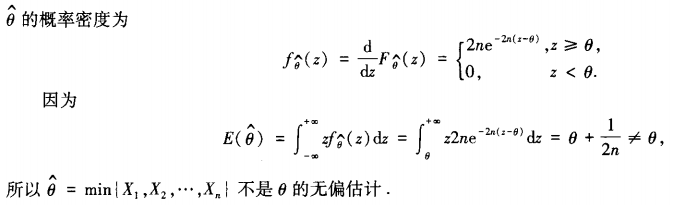
☛☛☛进入2022年研究生考试练习题库>>>更多考研试题(每日一练、模拟试卷、历年真题、易错题)等你来做!
扫码进入考研交流群
☟☟☟



