[单选题]设向量β可由向量组α1，α2，…αm线性表示，但不能由向量组(Ⅰ)：α1，α2，…，αm-1线性表示，记向量组(Ⅱ)：α1，α2，…，αm-1，β，则()。

　　A.αm不能由(Ⅰ)线性表示，也不能由(Ⅱ)线性表示

　　B.αm不能由(Ⅰ)线性表示，但可由(Ⅱ)线性表示

　　C.αm可由(Ⅰ)线性表示，也可由(Ⅱ)线性表示

　　D.αm可由(Ⅰ)线性表示，但不可由(Ⅱ)线性表示

　　参考答案：B

　　[单选题]设线性无关的函数y1，y2与y3均为二阶非齐次线性微分方程的解，C1和C2是任意常数，则该非齐次线性微分方程的通解是()。

　　A.

　　B.

　　C.

　　D.

　　参考答案：C

　　[单选题]设二次型在正交变换x=Py下的标准形为，其中，若，则在正交变换x=Qy下的标准形为()。

　　A

　　B

　　C

　　D

　　参考答案：A

　　[问答题]

　　求极限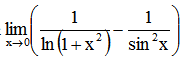

　　.

　　参考答案：

　　[问答题]设f(x)在区间[a，b]上连续，在(a，b)内可导，且f(a)=f(b)，f(x)不恒为常数证明：在(a，b)内至少存在一点，使得。

　　参考答案：因f(a)=f(b)，且f(x)不恒为常数，所以至少存在一点c∈(a,b)，使f(c)≠f(a)=f(b)。不妨设f(c)>f(a)，则在[a，c]上，由拉格朗日中值定理，至少存在一点东，使得

进入焚题库 领取备考资料

　　☛☛☛进入2022年研究生考试练习题库>>>更多考研试题(每日一练、模拟试卷、历年真题、易错题)等你来做!

扫码进入考研交流群

☟☟☟