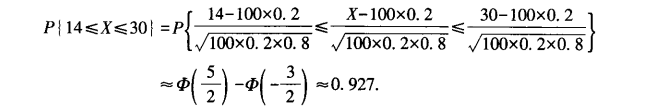[单选题]设X1，X2，…，Xn(n>1)相互独立同分布，概率密度为f(x)=2x-3，x≥1，i=1，2，…，则有()。

　　A.对每一个Xi都满足切比雪夫不等式

　　B.Xi都不满足切比雪夫不等式

　　C.X1，X2，…，Xn满足切比雪夫大数定律

　　D.X1，X2，…，Xn不满足辛钦大数定律

　　参考答案：B

　　[单选题]设X1，X2，…，Xn相互独立，且Xi(i=1，2，…，n)服从参数为λ(>0)的泊松分布，则下列选项正确的是()。

　　A.

　　B.

　　C.

　　D.

　　参考答案：A

　　[单选题]设随机变量X1，X2，…，Xn相互独立，则根据列维-林德伯格中心极限定理，当n充分大时，X1+X2+…+Xn近似服从正态分布，只要Xi(i=1，2，…)满足条件()。

　　A.具有相同的数学期望和方差

　　B.服从同一离散型分布

　　C.服从同一连续型分布

　　D.服从同一指数分布

　　参考答案：D

　　[问答题]设随机变量X和Y的数学期望都是2，方差分别为1和4，而相关系数为0.5，则根据切比雪夫不等式，有P{|X-Y|≥6}≤()。

　　参考答案：

　　[问答题]在每次试验中，事件A发生的可能性是0.5，则1000次独立试验中，事件A发生的次数在400次到600次之间的概率≥()。

　　参考答案：应填0.975。

　　[问答题]设随机变量X1，X2，…，Xn相互独立同分布，且=ak(k=1，2，3，4)，证明当n充分大时随机变量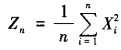近似服从正态分布，并指出其分布参数。

　　参考答案：

　　[问答题]某保险公司多年的统计资料表明，在索赔客户中被盗索赔占20%，以X表示在随机抽查的100个索赔客户中因被盗向保险公司索赔的户数。(1)写出X的概率分布;(2)利用德莫弗-拉普拉斯定理，求被盗索赔客户不少14户且不多于30户的概率的近似值。

　　 参考答案：【解】(1)X~B(100，0.2)。

　　(2)由棣莫弗-拉普拉斯中心极限定理，得：