2022年考研《数学一》考点习题:常微分方程
来源 :中华考试网 2021-03-27
中 [单选题]已知 是微分方程
是微分方程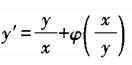 的解,则
的解,则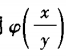 =()。
=()。
A.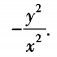
B.![]()
C.![]()
参考答案:A
[单选题]设线性无关的函数y1,y2与y3均为二阶非齐次线性微分方程的解,C1和C2是任意常数,则该非齐次线性微分方程的通解是()。
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:C
[单选题]如果函数y1(x)与y2(x)都是以下四个选项给出方程的解,设C1与C2是任意常数,则y=C1y1(x)+C2y2(x)必是()的解。
A.![]()
B.![]()
C.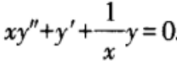
D.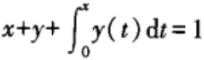
参考答案:C
[单选题]设![]() 是某二阶常系数非齐次线性微分方程的解,则该方程的通解是()。
是某二阶常系数非齐次线性微分方程的解,则该方程的通解是()。
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:A
[单选题]设y1(x)和y2(x)是微分方程y"+p(x)y+q(x)y=0的两个特解,则由y1(x),y2(x)能构成该方程的通解的充分条件为()。
A.y1(x)y’2(x)-y'1(x)y2(x)=0
B.y1(x)y’2(x)-y2(x)y1(x)≠0
C.y1(x)y’2(x)+y'1(x)y2(x)=0
D.y1(x)y’2(x)+y2(x)y1(x)≠0
参考答案:B
[单选题]微分方程y’’-y=ex+x的特解形式为y*=()。
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:B
[问答题]设y=ex是微分方程xy’+p(x)y=x的一个解,求此微分方程满足条件参考答案:将y=ex代入原方程,得xex+p(x)ex=x,解得p(x)=xe-x-x。方程化为y’+(e-x-1)y=1。
由通解公式,有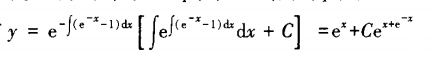
由![]() ,故所求特解为
,故所求特解为![]()
扫码进入考研交流群
☟☟☟

| 2022年研究生考试题库 | ||
|
考试题库 |
2022年考研《政治》考试题库|手机做题 | 在线做题 |
| 2022年考研《数学》考试题库|手机做题 | 在线做题 | |
| 2022年考研《英语》考试题库|手机做题 | 在线做题 | |


