施工进度计划的编制方法(重点)

　　n 横道图是一种最简单并运用最广的传统的进度计划的方法。将项目的进展表示在时间表格上，

　　横道图用于小型或大型项目子项目上，或用于计算资源需要量、概要预示进度、其他计划技术的表示结果

　　优点：表达方式较直观，易看懂计划编制的意图。

　　缺点：工序(工作)之间的逻辑关系不易表达清楚;

　　适用于手工编制计划;

　　不能确定计划的关键工作、关键路线与时差;

　　计划调整只能用手工方式进行，其工作量较大;

　　难以适应大的进度计划系统。

　　P118双代号网络计划

　　(1)节点：表示工作之间的连接状态，(起点节点、终点结点、中间结点)

　　一个网络计划只能有唯一的一个起点节点和唯一的一个终点节点(绘图规则)

　　每个节点必须都有编号，且编号从小指向大，可以不连续，但不能有重复

　　(2)箭线：表示一个施工过程或一道工序，

　　实箭线表示一项实实在在的工序(一定占用时间或消耗资源)

　　虚箭线表示并不存在的虚工作(既不消耗时间也不消耗资源，只是用来表示工作之间的逻辑关系(工艺关系和组织关系)，它起着工作之间联系、区分和断路的作用

　　箭线不能直接交叉，可通过指向圈或过桥形式

　　(3)工作：用箭线和两端带编号的节点表示工作，

　　实工作、 虚工作：

　　紧前工作：以该工作的开始节点为完成节点的所有工作

　　紧后工作：以该工作的完成节点为开始节点的所有工作

　　(5)线路：从网络计划的起点节点开始沿箭线方向到达终点节点的通路

　　网络计划不允许有循环回路(绘图规则)

　　关健线路：在网络计划的所有线路中所有工作持续时间之和最长的线路

　　关健线路上的工作是关健工作，

　　一个网络计划有多条线路，可有多条关健线路，但至少有一条关健线路

　　网络计划中的关健线路会发生转移，改变关健工作或非关健工作的持续时间，关健线路可能会变成非关健线路

　　(6)工期：计算工期(根据网络计划时间参数计算而得的工期)用Tc表示

　　要求工期(委托合同的工期)用Tr表示

　　计划工期(根据计划工期和要求工期，任务实施者结合实际情况确定的工期)用Tp表示、

　　当有要求工期时，Tp≦Tr、当无要求工期时，Tp=Tc

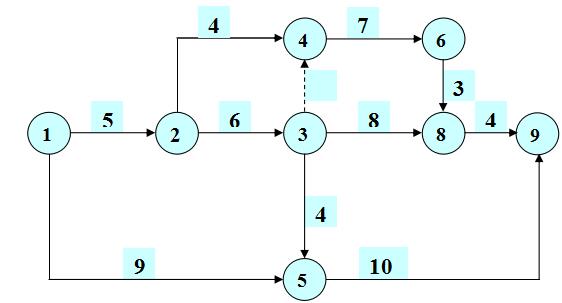
　　n 双代号网络计划的 时间参数

　　(1)Di-j ---工作持续时间

　　(2)ESi-j----最早开始时间：所有紧前工作全部完成后，本工作有 可能开始 的最早时间

　　(3)EFi-j---最早完成时间：所有紧前工作全部完成后，本工作有 可能完成 的最早时刻

　　最早完成时间= 最早开始时间+持续时间

　　(4)LSi-j--最迟开始时间：在不影响整个任务完成的前提下，本工作 必须开始 的最迟时刻

　　(5)LFi-j-最迟完成时间：在不影响整个任务完成的前提下，本工作 必须完成 的最迟时刻

　　最迟完成时间= 最迟开始时间+持续时间

　　(6) TFi-j--总时差： 在不影响总工期的前提下，本工作所拥有的机动时间

　　(7)FFi-j--自由时差：在不影响紧后工作最早开始时间的前提下，本工作的机动时间

　　n 六个时间参数的计算

　　(1)从 左向右 求得 最早开始时间、最早完成时间、网络的计算工期

　　顺求取大(当某工作有多项紧前工作时，其最早开始时间取所有紧前工作最早完成时间的最大值)

　　(2)从 右向左 求得 最迟完成时间、最迟开始时间、

　　逆求取小(当某工作有多项紧后工作时，其最迟完成时间取所有紧后工作最迟开始时间的最小值

　　总时差 =本工作最迟完成时间 -早完成时间(最迟开始时间-最早开始时间) 迟减早

　　自由时差 =紧后工作的最早开始时间 -本工作的最早完成时间 早减早( 有多项紧后工作取差值的最小值)

　　(3)确定 关健线路 ：至始至终由 总时差最小 的工作组成的线路

　　所有工作 持续时间最长 的线路

　　确定 关健工作 ： 总时差最小 的工作(只有当Tp=Tc时，TFi-j=0的工作才是关健工作，)

　　关健线路上 的工作

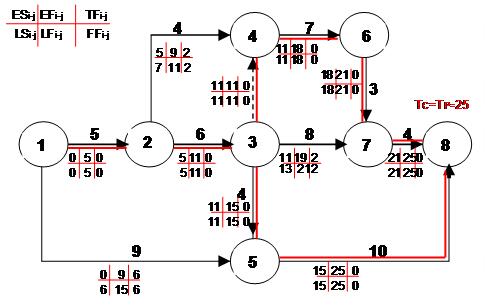
　　n 题型1 ： 网络图挑错 PPT 117. 118

　　n 题型2 ： 找关健线路 PPT 120

　　n 题型3 (1分的单选)121. 122 252

　　n 题型4 ： 关于关健工作和关健线路的说法

　　关于关健工作的说法：

　　l 总时差最小的工作为关健工作 对

　　l 总时差为0的工作为关健工作 错

　　只有当网络计划的Tp=Tc 时总时差为0的工作才是关健工作

　　当要求工期小于计算工期时总时差最小为负值

　　当要求工期大于计算工期时，总时差最小值为正值

　　l 关健线路上的工作是关健工作 对

　　l 工作的最迟完成时间与最早完成时间之差(最迟开始时间与最早开始时间之差)最小的工作为关健工作 对

　　l 自由时差最小的工作不一定是关健工作 对

　　l 双代号网络计划中持续时间最长的工作 错

　　关于关健线路的说法：

　　l 持续时间最长的线路是关健线路 对

　　l 在双代号网络计划中，当 Tp=Tc时，自始至终由总时差为0的工作组成的线路是关健线路 对

　　l 由总时差(自由时差)为0的工作组成的线路是关健线路 错

　　l 总时差最小的线路是关健线路 错

　　l 在 网络计划 中至始至终由关键工作组成的线路是关健线路 错

　　(因在单代号网络中就不适用)

　　l 在 双代号网络计划 中至始至终由关键工作组成的线路是关健线路 对

　　l 网络中的关健线路会在工作的实施中发生变化，由关健线路变成非关健线路 对

　　l 一 个网络图中至少有一条关健线路，如果有多条关健线路，则它们的持续时间一定相等 对

　　双代号网络计划在案例中 运用总时差判定索赔工期： (PPT 123 124)

　　l 如果延误的工作是关健工作，则不论延误几天，均会对后续工作和总工期产生影响，延误几天影响总工期几天

　　l 如果延误的工作是非关健工作，

　　超过其拥有的总时差，影响总工期的天数则为二者之差，

　　未超过总时差，则不影响总工期，

　　对后续工作的影响与其拥有的自由时差相比，延误时间超过自由时差，影响的天数为二者之差，未超过自由时差，则不影响紧后工作

　　P131 双代号时标网络计划

　　l 双代号时标网络计划是以 时间坐标为尺度 编制的网络计划。

　　l 时标网络中的 波形线 表示工作的 自由时差

　　l 时标网络关键线路 ( 至始至终没有波形线的线路 )

　　l 时标网络计划中 虚工作必须以垂直方向的虚箭线表示 ， 虚工作也会有自由时差

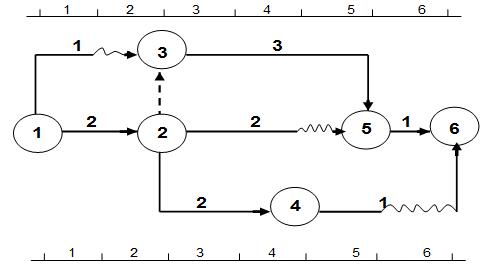
　　l 题型1： 从双代号时标网络图中可以直接看出：

　　工作的最早开始和完成时间

　　工作的自由时差

　　网络的关健线路

　　网络的计算工期

　　关健工作

　　l 题型2： 计算总时差和自由时差 PPT 125

　　l 在案例中应用：当某工作拖延，判定是否影响总工期或紧后工作的开始时间

　　P126 单代号网络 计划

　　单代号网络图是 以节点及编号表示工作 ，以 箭线表示工作之间逻辑关系(既不占用时间，也不消耗资源)

　　单代号网络图与双代号网络图相比，具有以下特点：

　　1、工作之间的逻辑关系容易表达，且不用虚箭线，故绘图较简单;

　　2、网络图便于检查和修改;

　　3、由于工作持续时间表示在节点之中，没有长度，故不够形象直观;

　　4、表示工作之间逻辑关系的箭线可能产生较多的纵横交叉现象。

　　n 时间参数的计算：

　　(1)从 左往右 算 顺求取大 求得最早(开始、完成)、求得网络计划的计算工期

　　(2) 计算 各工作之间的 时间间隔

　　(LAG i,j )( 紧后 工作的 最早开始 时间- 本工作 的 最早完成 时间)

　　(3) 确定关健线路 : 从网络计划的终点开始依次将LAG i,j =0的线路连接至起点、 由关健工作组成 且 相邻工作之间的时间间隔为0的线路

　　持续时间最长 的线路是关健线路

　　(4)计算工作的自由时差(该工作与紧后工作之间时间间隔)(有多项紧后工作取最小值 )

　　(5)计算工作的总时差：(逆算)等于紧后工作的总时差+其与紧后工作的时间间隔之和(有多项紧后工作取最小值)

　　n 题型1： 找关健线路，关健工作 示例

　　n 题型2： 求工作的时间间隔 示例