第8章 钢筋混凝土构件正常使用极限状态验算

　　一、抗裂验算

　　抗裂就是不容许出现裂缝。对于一旦开裂就会严重影响使用性或耐久性的结构，应进行抗裂验算，采取措施保证其在正常使用阶段不开裂。

　　1、轴心受拉构件的抗裂验算

　　根据轴心受拉构件的抗裂极限状态：混凝土的拉应力σc=ft(教材图8-1)，拉应变εc =εtu;钢筋拉应力可根据钢筋和混凝土应变相等的关系求得σs=εsEs=εcEs =αEεtuEc=αEft。对换算截面面积A0= Ac+αEAs(这样才好利用力学中的匀质弹性体分析方法)，由力的平衡条件可求得即将发生裂缝时的抗裂轴向拉力：

　　Ncr= Acft+σs As= Acft+αEft As= ft(Ac +αE As)= ft A0

　　在正常使用极限状态验算时，考虑目标可靠指标的要求，引进一个拉应力限制系数αct，形成有限拉应力状态，并且混凝土抗拉强度取用标准值，荷载也取用标准值。所以，对于轴心受拉构件，在荷载效应的短期组合及长期组合下，应按下列公式分别进行抗裂验算：

　　Ns≤αct ftk A0

　　Nl≤αct ftk A0

　　2、受弯构件的抗裂验算

　　根据受弯构件的抗裂极限状态，即第3章讨论的受弯构件在第Ⅰ阶段末尾将开裂的Ⅰa状态计算构件抗裂弯矩Mcr(见下图a)

　　由于混凝土受拉区的塑性发展，拉应力图形为曲线形(见下图a)，可近似假定混凝土受拉区应力分布为见下图b所示的梯形，最终为分析方便，且能利用力学中的匀质弹性体计算方法，保持抗裂弯矩不变，转换为弹性应力分布(见下图c)。混凝土受拉区的塑性发展后，抗裂弯矩要大于弹性阶段(边缘混凝土的拉应力也是ft，但没有发展塑性)的值。因此，若转换为弹性应力分布，而要保持计算的抗裂弯矩不变，就必须改变应力图形的参数大小。这里在考虑塑性性质后，把弹性极限应力提高为γmft。

　　经过这样的换算，就可把构件视作截面面积为A0= Ac+αE As+αE A's的匀质弹性体，引用材料力学的公式，可得出受弯构件正截面抗裂弯矩Mcr的计算公式

　　Mcr=γmftkW0

　　同样，引进一个拉应力限制系数αct，在荷载效应的短期组合及长期组合下，按下列公式分别进行抗裂验算：

　　Ms≤αctftkγmW0

　　Ml≤αctftkγmW0

　　如果验算公式两边同除以截面特征值(轴拉为A0、受弯为W0)，实际相当于在荷载效应的短期组合和长期组合两种情况下，构件验算点拉应力不能超过由混凝土拉应力限制系数αct控制的应力值αctftk。偏心受力构件同样道理分析。

　　Ms( Ml)≤Mcr即满足抗裂要求。规范偏于安全出发用 αct对ftk进行了折减，也可宏观认为是对Mcr的折减。拉应力限制系数 αct的采用，实际上就是对混凝土抗拉强度标准值进行折减以控制截面应力不超过一更保守的限定值。短期组合和长期组合的概念见第2章。

　　3、偏心受力构件的抗裂验算

　　偏心受力构件可采用与受弯构件相同的方法分析计算抗裂性能，但关键是混凝土塑性影响系数γ的确定。

　　研究表明，偏心受拉构件受拉区塑化效应与受弯构件的塑化效应相比，有所减弱，这是因为它的受拉区应变梯度(受拉区边缘应变εtu与截面受拉区高度的比值。)比受弯构件的应变梯度要小。但它的塑化效应又比轴心受拉构件的大，因为轴心受拉构件的应变梯度为零(见教材图8-5)。因此，偏心受拉构件的塑性影响系数γ偏拉应处于γm(受弯构件的塑性影响系数)与1(轴心受拉构件的塑性影响系数)之间，可近似地认为γ偏拉是随截面的平均拉应力σ=Ns/ A0(σ=Nl/ A0)的大小，按线性规律在1与γm之间变化。

　　偏心受压构件由于受拉区应变梯度比较大，塑化效应比较充分，因而其塑性影响系数γ偏压比受弯构件的γm大。但在实际应用中，为简化计算并考虑偏于安全，取与受弯构件相同的数值，即取γ偏压=γm。

　　经变换后，就可得出偏心受力构件在荷载效应的短期组合和长期组合下的抗裂验算教材公式(8-19、8-19、8-22、8-23)。

　　γ反映了截面塑性发展对构件抗裂性能的影响程度。

　　4、提高构件抗裂能力的方法

　　分析表明，开裂之前钢筋应力是很低的(混凝土的拉应变很低，钢筋与混凝土在开

　　裂之前保持应变协调限制了钢筋应力的发展)，即对于钢筋混凝土的抗裂能力而言，钢筋所起的作用不大，对抗裂贡献是很有限的。所以用增加钢筋配筋率的办法来提高构件的抗裂能力是极不经济的，钢筋是在开裂后才有效发挥其限制裂缝作用。加大构件截面尺寸、特别是截面高度与提高混凝土的强度等级可有效提高构件抗裂能力。在混凝土中掺入纤维也可提高构件抗裂能力，最根本的方法是采用预应力混凝土结构，但这实际已超出普通钢筋混凝土结构的范围。

　　二、裂缝宽度验算

　　不必要求抗裂的构件，就可以放宽标准，允许其出现裂缝。但如果裂缝过宽，则会降低混凝土的抗渗性和抗冻性等使用功能，进而影响结构的耐久性和外观，并会引起使用者心理不安。因此，对这种构件就必须进行裂缝宽度验算，限制其裂缝宽度过大。

　　1、引起裂缝的因素

　　(1)荷载。荷载引起的混凝土的拉应变达到混凝土的极限拉应变时，混凝土就会开裂。

　　(2)非荷载因素。温度变化，混凝土收缩，基础沉降，混凝土塑性坍塌，钢筋锈蚀，碱—骨料化学反应等非荷载因素引起的变形受到约束时，就可能产生裂缝。

　　非荷载作用引起的裂缝目前还无法准确计算，但可从材料、设计和施工等方面采取措施予以减轻其危害。

　　三、变形验算

　　1、钢筋混凝土梁变形计算的特点

　　对于匀质弹性材料梁，当梁的截面尺寸和材料确定后，截面的抗弯刚度EI就为常数了，然后可按《材料力学》的公式计算变形。由下图可知，钢筋混凝土梁由于塑性变形的出现以及裂缝的产生和发展，导致变形模量降低和截面惯性矩下降，使截面的抗弯刚度随着荷载的增加而不断降低。

　　对其正常使用状况下的挠度进行计算时，采用恒定的刚度EI就不能反映梁的实际工作情况。所以规范用抗弯刚度B取代式中的EI，B是随弯矩M的增大而减小的变量。分析表明，刚度B确定后仍可按材料力学的计算公式计算梁的挠度。所以，钢筋混凝土梁的变形(挠度)计算就归结为抗弯刚度B的计算。

　　2、受弯构件的短期刚度Bs

　　(1)不出现裂缝的构件

　　Bs=0.85EcI0

　　0.85——考虑混凝土出现塑性时弹性模量的降低系数。此为阶段Ⅰ的刚度计算。

　　(2)出现裂缝的构件

　　Bs=(0.025+0.28αEρ)(1+0.55γ'f+0.12γf)Ecbh03

　　3、受弯构件的长期刚度Bl

　　在荷载长期作用下，钢筋混凝土梁受压区混凝土将产生压缩徐变，受拉区混凝土与钢筋之间将产生粘结滑移徐变，使受拉混凝土不断退出工作，即使荷载不增加，挠度也将随时间的增加而增大。混凝土收缩也会造成梁刚度降低、变形增大。因此需要得到长期刚度Bl，以求最大挠度值。

　　(1)荷载效应的短期组合(并考虑部分荷载长期作用影响)的刚度

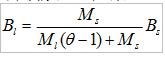
　　(2)荷载效应的长期组合的刚度

　　Bl= Bs/θ

　　4、最小刚度原则

　　构件的截面刚度随截面的内力和配筋大小而变，即沿构件跨度方向各截面刚度不等。为简化起见，在按材料力学方法计算受弯构件的变形时，取同号弯矩区段内截面的最小刚度作为该区段的平均刚度，而按等刚度或分段等刚度的构件进行计算。

　　5、提高刚度的方法

　　若验算挠度不能满足规范要求时，则表示构件的抗弯刚度不足。可以通过增加截面尺寸、提高混凝土强度等级、适当增加配筋量和选用合理的截面(如T形或工形等)的方法来提高刚度。但合理而有效的措施是适当增大截面的高度。采用预应力混凝土结构也可有效提高构件刚度。

　　这里计算时，要把荷载效应组合的概念真正弄懂。在第2章已经讲过，短时间内，可能存在所有对结构不利的荷载都出现的组合，当然是指的变化着的活荷载的短时共存，再叠加上必然存在的永久荷载，这就是荷载效应的短期组合。也就是说此组合中，长、短期荷载都有，所以可称为荷载效应的短期组合(并考虑部分荷载长期作用影响)的情况，承载力计算也只用到此组合。而荷载效应的长期组合中，只有长期作用性质的那部分荷载，即可由短期组合中，把短时间内存在的活荷载去掉，只保留长期作用永久荷载和可变荷载准永久值。所以，可以知道：短期组合的载准值实际包含了长期组合的载准值。

　　四、混凝土结构的耐久性

　　结构的耐久性是指结构在使用环境下，对物理的、化学的以及其他使结构材料性能恶化的各种侵蚀的抵抗能力。混凝土结构的耐久性问题越来越受到人们的重视。在设计混凝土结构时，除了进行承载力计算、变形和裂缝验算外，还必须进行耐久性设计。

　　由于影响因素的复杂，目前混凝土结构的耐久性设计实质上是针对影响耐久性能的主要因素提出相应的对策，即以概念设计为主。一般是采取措施一定来保证耐久性，提高耐久性的主要措施有：

　　合理加大混凝土保护层的最小厚度;严格按规范控制裂缝宽度;注意保证混凝土原材料的质量;提高混凝土的密实度;采用耐腐蚀钢筋;在结构表面设置专门的防渗面层等。

　　正常使用极限状态验算的基本概念一定要清楚，要看懂课本例题，会用基本公式进行计算。