参考答案

　　一、判断题

　　1、

　　【正确答案】 错

　　【答案解析】

　　本题考查的是现金流量图。如果现金流出或流入不是发生在计息周期的期初或期末，而是发生在计息周期的期间，为了简化计算，公认的习惯方法是将其代数和看成是在计息周期的期末发生，称为期末惯例法。参见教材P147。

　　2、

　　【正确答案】 错

　　【答案解析】

　　本题考查的是房地产投资活动共的现金流量。房地产投资信托基金常采用“购买-持有出租-出售”的模式。参见教材P149。

　　3、

　　【正确答案】 错

　　【答案解析】

　　本题考查的是资金时间价值的概念。资金一旦用于投资就不能用于即期消费，所以，从消费者的角度来看，资金的时间价值体现为放弃即期消费的损失所应得到的必要补偿。参见教材P151。

　　4、

　　【正确答案】 对

　　【答案解析】

　　本题考查的是利息与利率。平均利率是一个纯理论的概念。在现实生活中，人们面对的是市场利率而非平均利率。参见教材P154。

　　5、

　　【正确答案】 错

　　【答案解析】

　　本题考查的是单利计息与复利计息。从理论上讲，资金在不停地运动，每时每刻都在通过生产和流通领域增值，因而应该采用连续复利计息，但是在实际使用中都采用较为简便的间断复利计息方式计算。参见教材P156。

　　6、

　　【正确答案】 错

　　【答案解析】

　　本题考查的是名义利率与实际利率。现值计算，如果名义利率相同，计息周期不同，则未来某个时点上两笔等额资金的现值不一定相等。参见教材P156～157。

　　7、

　　【正确答案】 错

　　【答案解析】

　　本题考查的是名义利率与实际利率。名义利率是指一年内多次计息时给出的年利率，它等于计息周期利率与一年内计息周期数的乘积。参见教材P156。

　　8、

　　【正确答案】 错

　　【答案解析】

　　本题考查的是名义利率与实际利率。名义利率越大，计息周期越短，实际利率与名义利率的差异就越大。参见教材P157。

　　9、

　　【正确答案】 错

　　【答案解析】

　　本题考查的是名义利率与实际利率。运用公式i=(1+r/m)m-1，在m不变时，名义利率r越大，实际利率i就越大。参见教材P157。

　　10、

　　【正确答案】 对

　　【答案解析】

　　本题考查的是名义利率与实际利率。实际利率=(1+名义利率/计息周期数)计息周期数-1=(1+5%/4)4-1=5.09%。参见教材P157。

　　11、

　　【正确答案】 对

　　【答案解析】

　　本题考查的是资金等效值的概念。资金等效值是指在考虑时间因素的情况下，不同时点发生的绝对值不等的资金可能具有相同的价值。参见教材P157。

　　12、

　　【正确答案】 对

　　【答案解析】

　　本题考查的是复利计算。年值是指连续出现在各计息周期期末的等额支付金额。参见教材P158。

　　13、

　　【正确答案】 错

　　【答案解析】

　　本题考查的是复利计算。等额序列支付现值系数与等额序列支付资金回收系数互为倒数，两者之积为1。参见教材P159。

　　14、

　　【正确答案】 对

　　【答案解析】

　　本题考查的是复利系数的应用。次贷危机的原因相当复杂，并不单单是一个住房价格下跌的因素。参见教材P168。

　　二、计算题

　　1、

　　【正确答案】 (1)抵押贷款额P=100×50%=50万元;

　　月贷款利率i=12%/12=1%;

　　月还款额为：A= P×i(1+i)n/[(1+i)n-1]= 50×1%(1+1%)240/[(1+1%)240-1]=5505.43元;

　　(2)该家庭欲购买上述住宅，其月收入须为：5505.43/30%=18351.43元

　　(3)该家庭在第6年年初一次提前偿还剩余贷款余额时，所需偿还金额为

　　Pn=A[((1+i)n-m-1)/[i(1+i)n-m]，其中，n=12×20=240，m=12×5=60，

　　代入数据，得到Pn=5505.43×[((1+1%)240-60-1)/[1%(1+1%)240-60]=458721.59元。

　　2、

　　【正确答案】 第一步：计算出贷款总额

　　P=120×7800×(1-30%)=65.52(万元)

　　第二步：计算出商业贷款的总额

　　P1=65.52-20=45.52(万元)

　　第三步：计算出商业贷款的月还款额A1。

　　。

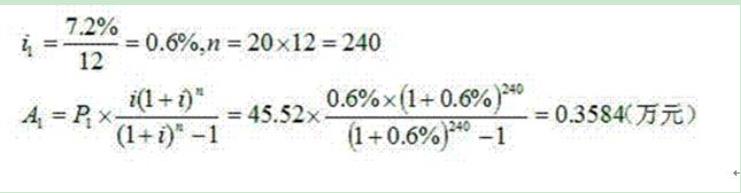
　　【答案解析】

　　3、

　　【正确答案】 贷款余额=第6年至第10年的年值，折现到第5年年末时的现值。

　　4、

　　【正确答案】 (1)已知P=8000万元，n=20年，i=27%，S=10%，t=8;

　　(2)由A1=P×(i-s)/(1-[(1+s)/(1+i)]n)可得：

　　A1=8000×(27%-10%)/{1-[(1+10%)/(1+27%)]20)=1441.4(万元);

　　(3)利用公式At=A1(1+s)t-1，可得A8=1441.4×(1+10%)8-1=2808.9(万元)

　　该写字楼第八年的净租金收入达到2808.9万元以上时，方能满足投资者收益目标的要求。

　　5、

　　【正确答案】 (1)月还款额=7000×25%=1750元，月利率=6%/12=0.5%;

　　购买住房最高额=最高贷款额/70%

　　=(1750/0.5%)×[1-1/(1+0.5%)12×20]/70%=34.9(万元)(套用“等额序列支付的现值计算公式”)

　　(2)月利率=9%/12=0.75%，套用“等额序列支付的现值计算公式”

　　按6%利率计算第6年年初还剩的货款总额=1750/0.5%×[1-1/(1+0.5%)180]=207381.15

　　按9%利率计算月还款1750元相当的货款总额=1750/0.75%×[1-1/(1+0.75%)180]=172538.47

　　则为保持原月偿还额不变，第6年年初需要一次性还款额=207381.15-172538.47=34842.68(元)

　　(3)若不提前偿还贷款，设需要偿还的年限为n

　　207381.15=(1750/0.75%)×[1-1/(1+0.75%)12n]

　　则n=24.5年

　　延长期=24.5-15=9.5(年)