[单选题]已知a>b，则下列等式恒成立的是()。

　　Aa²>b²

　　B>1

　　C<

　　D5a>5b

　　参考答案：D

　　[单选题]下列函数中，为奇函数的是()。

　　Ay=

　　By=-2x+3

　　Cy=x2-3

　　Dy=3cosx

　　参考答案：A

　　[单选题]已知向量|a|=3，|b|=4，且a和b的夹角为120°，则a·b=()。

　　A

　　B

　　C6

　　D-6

　　参考答案：D

　　[单选题]已知α为三角形的一个内角，且sinα+cosα=则α∈()。

　　 A

　　B

　　C

　　D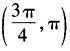

　　参考答案：C

　　[问答题](填空题)函数y=2x(x+1)在x=2处的切线方程是__________.

　　参考答案：

　　10x-y-8=0由函数y=2x(x+1)

　　知，y´=(2x2+2x)'=4x+2，则y´|x=2=10.又当x=2时，y=12，知此函数的切线过点(2，12)，且斜率为10。则其切线方程为10(x-2)=y-12，即10x-y-8=0.

　　[问答题](填空题)函数y=x3-2x2-9x+31的驻点为__________.

　　参考答案：

　　[问答题]与已知直线7x+24y-5=0平行，且距离等于3的直线方程是______。

　　参考答案：

　　7x+24y+70=0或7x+24y-80=0

　　[问答题]

　　参考答案：

　　[问答题]已知二次函数ƒ(x)=ax2+bx+c的图象C与x轴有两个交点，它们之间的距离为6，C的对称轴方程为x=2，且ƒ(x)有最小值-9，求： (Ⅰ)a，b，c的值; (Ⅱ)如果ƒ(x)不大于7，求对应x的取值范围.

　　参考答案：

　　(Ⅰ)由已知，抛物线的顶点坐标为(2，-9)，则可设所求函数的解析式为ƒ(x)=a(x-2)2-9，由对称性知，抛物线过点(5，o)，将2=5，y=0代入所设解析式，得9a-9=0，解得a=1.因为ƒ(x)=(x-2)2-9，即ƒ(x)=x2-4x-5，

　　所以a=1，b=-4，c=-5.

　　(Ⅱ)由已知ƒ(x)≤7，即x2-4x-5≤7，x2-4x-12≤0，解得-2≤x≤6.

2022年成人高考高起点考试题库|手机做题

限时优惠购买

　　2022年成人高考题库章节练习、每日一练、模拟试题、历年真题，扫描下方二维码获取【焚题库小程序】免费试做。