[问答题]空间有四个点，如果其中任何三点不在同一直线上，可以确定几个平面?

　　参考答案：

　　根据公理，在所给定的四点中任取三点，可确定一个平面，由组合公式

　　所以共可确定四个平面。 [问答题]已知空间四边形OABC，OB=OC且∠AOB=∠AOC=θ(如图)

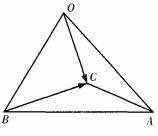
　　。求证：OA⊥BC。

　　参考答案：

　　[问答题]ABCD是正方形，E是AB的中点，如将△DAE和△CBE分别沿虚线DE、CE折起，使AE与BE重合如图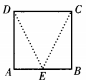，设A与B重合后的点为P，则面PCD与面ECD所成的二面角为______度，PE与面ECD成______度。

　　参考答案：

　　二面角为30°，PE与面ECS成60角°

　　参考解析：

　　(1)求面PCD与面ECD所成的二面角为多少度，就是要求出由平面PCD与平面ECD所组成的二面角的平面角，其中画出二面角的平面角是关键，因为二面角确定以后，二面角的平面角很容易画出(由二面角的平面角的定义)。求角度时，常用到勾股定理、正弦定理、余弦定理、兰垂线定理和逆定理。

　　(2)求PE与面ECD成多少度，就是求直线与平面所成的角是多少度。首先要找出平面的一条斜线(直线PE)和斜线的射影，斜线和射影所成的锐角，就是直线PE和平面ECD所成的角，再求出角度。

　　设CD的中点为F，练PF，EF

　　∵PC=PD，EC=ED

　　∴PF⊥CD，EF⊥CD(三垂线定理)

　　∠PFE是二面角P-CD-E的平面角

　　∵PE⊥PC，PE⊥CD

　　∴PE⊥平面PCD，又PF在平面PCD内

　　∴PE⊥PF

　　设正方形边长为1(如图)

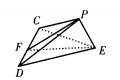
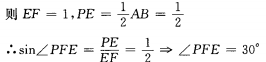
　　故面PCD与面ECD所成的二面角为30°，PE与面ECS成60角°。

　　[问答题]如图

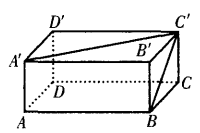
　　，已知长方体的长和宽都是4cm，高是2cm。求

　　(1)BC和A’C’所成的角是多少度?

　　(2)A’B’和DD’的距离是多少? 参考答案：

　　(1)在长方体中BC和A’C’不在同一个平面内

　　所以BC和A’C’是异面直线

　　∵在长方体中BC//B’C’

　　∴∠A’C’B’是异面直线BC和A’C’所成的角

　　∵A’C’B’=45°

　　异面直线BC和A’C’所成的角是45°

　　(2)A’B’和DD’是异面直线

　　∵A’D’⊥A’B’ A’D’⊥DD’

　　∴A’D’的长即为异面直线A’B’和DD’的距离

　　∵A’D’=4

　　∴A’B’和DD’间的距离为4cm。

2021年成人高考高起点考试题库|手机做题

限时优惠购买

　　2021年成人高考题库章节练习、每日一练、模拟试题、历年真题，扫描下方二维码获取【焚题库小程序】免费试做。