投资理论

　　相关推荐：2017年银行从业资格考试知识点讲义大全（各科目）

　　(一)收益与风险

　　1.持有期收益和持有期收益率

　　投资的时间区间就是持有期，持有期间的收益就是持有期收益(HPR)。相应的持有期收益率(HPY)就是持有期间的收益率。在数值上等于持有期间所获得的全部收益与初始投资的比率。

　　(1)面值收益=红利+市值变化

　　(2)收益率(百分比收益)=面值收益/初始市值=红利收益+资本利得收益

　　【教材例题】张先生去年初以每股25元的价格购买了100股中国移动的股票，过去一年中得到每股0.2元的红利，年底时以每股30元的价格出售，其持有期收益和收益率分别为多少?

　　『正确答案』

　　期初投资额为25×100=2500(元)

　　年底股票价格为30×100=3000(元)

　　现金红利为0.20×100=20(元)

　　则持有期收益为20+(3000-2500)=520(元)

　　持有期收益率为520/2500=20.8% 　　2.预期收益率

　　预期收益率是指投资对象未来可能获得的各种收益率的平均值。

　　任何投资活动都是面向未来的，而未来具有不确定性，因此投资收益也具有不确定性。也就是具有风险。但为了便于比较，可以用预期收益(期望收益)来描述。

　　预期收益率的计算公式：

　　E(Ri)=(P1R1+P2R2+……PnRn)×100%=∑PiRi×100%

　　其中：Ri为投资可能的投资收益率;

　　Pi为投资收益率可能发生的概率。

　　【教材例题】关于预期收益率的计算

　　『正确答案』E(Ri)=[0.15×0.2+0.15×(-0.2)+0.7×0.1]×100%=7%

 　　3.风险的测定

　　风险是指未来收益的不确定性。可以用方差和标准差来表示。

　　(1)方差：是一组数据偏离其平均值的程度。

　　公式：σ2=∑Pi×[Ri-E(Ri)]2

　　方差越大，这组数据就越离散，数据的波动也就越大;方差越小，这组数据就越聚合，数据的波动也就越小。

　　(2)标准差σ：方差的开平方为标准差，即一组数据偏离其均值的平均距离。

　　【教材例题】计算方差和标准差

　　『正确答案』

　　σ2=∑Pi×[Ri-E(Ri)]2=

　　0.15×0.0169+0.15×0.0729+0.70×0.0009=0.0141

　　σ=0.1187

　　(3)变异系数。变异系数CV=标准差/预期收益率=σi/E(Ri)

　　变异系数(CV)描述的是获得单位的预期收益须承担的风险。变异系数越小，投资项目越优。

　　【教材例题】项目A和项目B的收益和风险状况如表所示，根据不同的收益率和标准差计算其变异系数，评价项目优劣。

　　『正确答案』CVA=0.07/0.05=1.40;CVB=0.12/0.07=1.71

　　CVA小于CVB，显然，项目A比项目B更优。

 　　4.必要收益率

　　概念：必要收益率是投资某投资对象所要求的最低回报率，也称必要回报率。

　　构成：时间价值+通货膨胀率+风险补偿率

　　产生必要回报率的原因

　　①时间补偿。投资者放弃当前消费而投资，应该得到相应补偿，即将来的货币总量的实际购买力要比当前投入的货币的实际购买力有所增加，在没有通货膨胀的情况下，这个增量就是投资的真实收益，即货币的纯时间价值。也叫真实收益率。

　　②通货膨胀的补偿。投资者预期价格在投资期内会上涨，即存在通货膨胀，他必将要求得到对于通货膨胀所造成的损失的补偿。

　　③风险补偿。投资者对投资的将来收益不能确定，他将要求对该不确定性进行补偿，即投资的风险补偿。

　　5.系统性风险和非系统性风险

　　(1)系统性风险也称宏观风险，是指由于某种全局性的因素而对所有投资项目(产品)都产生作用的风险。具体包括市场风险、利率风险、汇率风险、购买力风险、政策风险等。

　　(2)非系统性风险也称微观风险，是因个别特殊情况造成的风险，它与整个市场没有关联。具体包括财务风险、经营风险、信用风险、偶然事件风险等。

　　(二)资产组合理论

　　现代资产组合理论由美国经济学家哈里·马柯维茨提出的。l952年，哈里·马柯维茨在《投资组合选择》一文中，第一次提出了现代投资组合理论(也称均值一方差模型)。该理论描述了投资怎样通过资产组合，在最小风险水平下获得既定的期望收益率，或在风险水平既定的条件下获得最大期望收益率。

　　(1)资产组合理论原理

　　投资者或“证券组合”管理者的主要意图，是尽可能建立起一个有效组合。那就是在市场上为数众多的证券中，选择若干证券进行组合，以求得单位风险水平上的收益最高，或单位收益的水平上风险最小。

　　(2)资产组合的风险和收益

　　我们也可将证券组合视为一个资产，那么，资产组合的收益率和风险也可用期望收益率和方差来计量。

　　(3)证券组合风险和相关系数

　　两个或两个以上资产所构成的集合，称为资产组合。资产组合的预期收益率，就是组成资产组合的各种资产的预期收益率的加权平均数，其权数等于各种资产在整个组合中所占的价值比例。

　　一般而言，由于资产组合中每两项资产间具有不完全的相关关系，因此随着资产组合中资产个数的增加，资产组合的风险会逐渐降低。但当资产的个数增加到一定程度时，资产组合风险的下降将趋于平稳，这时资产组合风险的降低将非常缓慢直至不再降低。

　　对证券组合来说，相关系数可以反映一组证券中，每两组证券之间的期望收益做同方向运动或反方向运动的程度。理论上，用相关系数来反映两个随机变量之间共同变动程度。相关系数处于区间[一1，1]内。

　　(4)两种资产组合的收益率和方差

　　设有两种资产A和B，某投资者将一笔资金以XA的比例投资于资产A，以XB的比例投资于资产B，且XA+XB=1，称该投资者拥有一个资产组合P。如果期末时，资产A的收益率为rA，资产B的收益率为rB，则资产组合P的收益率为 rP=XArA+ XBrB 。

　　投资组合期望收益率E(A,B)= XArA+ XBrB，收益率方差D(A,B)=rA2×σA2+rB2×σB2+2 rArBσAσBρ =rA2×σA2+rB2×σB2+2 rArB COV(A,B)

　　式中：σAσBρ——协方差，记为COV(A,B)

　　(5)最优资产组合

　　一般而言，投资者在选择资产组合过程中遵循两条基本原则：一是在既定风险水平下，预期收益率最高的投资组合;二是在既定预期收益率条件下，风险水平最低的投资组合。

　　①投资者的个人偏好。

　　由于不同投资者对期望收益率和风险的偏好不同，当风险从σB增加到σA时，期望收益率将补偿E(rA)一E(rB)。是否满足投资者个人的风险补偿要求因人而异，从而按照他们各自不同的偏好对两种资产得出不同的比较结果。从对于这一补偿的态度上可以分为三类投资者：

　　投资者甲(中庸)认为，增加的期望收益率恰好能补偿增加的风险，所以A与B两种资产组合的满意程度相同，资产A与资产B无差异;

　　投资者乙(保守)认为，增加的期望收益率不足以补偿增加的风险，所以A不如B更令他满意;

　　投资者丙(进取)认为，增加的期望收益率超过对增加风险的补偿，所以A更令人满意，即A比B好。

　　在同样风险状态下，要求得到的期望收益率补偿越高，说明该投资者对风险越厌恶。上述三位投资者中乙最厌恶风险，因而他最保守;甲次之;丙对风险厌恶程度最低，最具冒险精神。

　　②无差异曲线。一个特定的投资者，任意给定一个资产组合，根据他对风险的态度，按照期望收益率对风险补偿的要求，可以得到一系列满意程度相同(无差异)的资产组合。如图2—1所示，某投资者认为经过A的那一条曲线上的资产组合与他的满意程度相同，那么，我们称这条曲线为该投资者的一条无差异曲线。

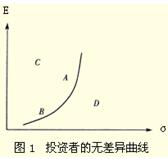
　　无差异曲线具有如下特点：

　　a.不同的无差异曲线不会相交。

　　b.无差异曲线的位置越高，它带来的满意程度就越高。

　　c.无差异曲线的条数是无限的而且密布整个平面。

　　d.无差异曲线是一簇互不相交的向上倾斜的曲线。一般情况下曲线越陡，表明风险越大，要求的边际收益率补偿越高。

　　不同投资者因为偏好不同，会拥有不同的无差异曲线族。图2—2是几个具有不同偏好的投资者的无差异曲线。

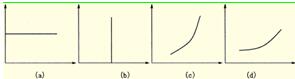
　　图2　不同偏好投资者的无差异曲线

　　图(a)的投资者对风险毫不在意，只关心期望收益率。图(b)的投资者只关心风险，风险越小越好，对期望收益率毫不在意。图(c)和图(d)表明一般的风险态度。图(d)的投资者比图(c)的投资者相对保守一些，相同的风险状态下，前者对风险的增加要求更多的风险补偿，反映在无差异曲线上，前者的无差异曲线更陡峭一些。

　　③最优资产组合的确定。

　　投资者的偏好通过他的无差异曲线来反映。无差异曲线位置越靠上，其满意程度越高，因而投资者需要在有效边缘上找到一个投资组合相对于其他有效组合处于最高位置的无差异曲线，该组合便是他最满意的有效组合。也就是说，最优资产组合是无差异曲线族与有效边缘的切点所在的组合。

　　(6)投资组合的管理

　　投资组合管理的根本任务是对资产组合的选择，即确定投资者认为最满意的资产组合。整个决策过程分成五步：资产分析、资产组合分析、资产组合选择、资产组合评价和资产组合调整。

　　①资产分析。它要求对资产的未来前景作出预测，这些预测必须将不确定性和相互关系考虑进去。

　　②资产组合分析。作出关于资产组合的预测，这种预测通过计算E(rP)和σP的数值来完成。

　　③资产组合选择。投资者或某个知悉投资者偏好的人按照该投资者的偏好选择最佳组合。

　　④资产组合评价。按一定标准和程序对选择出的最佳资产组合进行评判。

　　⑤调整资产组合。评判后如果不是最佳资产组合，则对资产组合进行调整，重复前面四个步骤。