自考《初中数学学科基础》章节习题：第3章

　　第三章：

　　一、简答题：

　　1、 试论数理统计方法的基本步骤。

　　用数理统计方法解决一个实际问题，一般有如下几个步骤 ：建立数学模型 ，收集整理数据，进行统计推断、预测和决策。当然，这些环节不能截然分开，也不一定按上述次序，有时是互相交错的。

　　(1)模型的选择和建立。

　　(2)数据的收集 。(3)安排特定实验以收集数据，这些特定的实验要有代表性，并使所得数据便于进行分析。(4)数据整理。(5)统计推断。(6)统计预测。(7)统计决策。

　　2、 如何理解概率和频率的关系。

　　在初中数学中，概率的概念是通过频率来介绍的。通常称为概率的‘统计’定义。事实上，这种定义只是一种描述性的说法，并不严格。因此，老师们一定不要去细究这种说法在用词上的含义。(在现代数学中，‘概率’是用公理化的方式给出的，超出了我们讨论的范围。)比如，我们说，当试验次数很多时，频率会‘稳定’在一个常数附近。什么叫‘稳定’就是含糊的。而且这个定义有‘循环定义’之嫌。当我们说，如果试验次数很多，频率偏离这个常数大的可能性很小时。这里的‘可能性’就是概率。(类似地，在古典概率中的‘等可能性’就是指概率相等。也是循环定义。)

　　4、(10分)小华与小丽设计了A、B两种游戏：游戏A的规则：用3张数字分别是2，3，4的扑克牌，将牌洗匀后背面朝上放置在桌面上，第一次随机抽出一张牌记下数字后再原样放回，洗匀后再第二次随机抽出一张牌记下数字.若抽出的两张牌上的数字之和为偶数，则小华获胜;若两数字之和为奇数，则小丽获胜。游戏B的规则：用4张数字分别是5，6，8，8的扑克牌，将牌洗匀后背面朝上放置在桌面上，小华先随机抽出一张牌，抽出的牌不放回，小丽从剩下的牌中再随机抽出一张牌.若小华抽出的牌面上的数字比小丽抽出的牌面上的数字大，则小华获胜;否则小丽获胜。

　　请你帮小丽选择其中一种游戏，使她获胜的可能性较大，并说明理由.

　　用列表法

所有可能出现的结果共有9种，其中两数字之和为偶数的有5种，所以游戏A小华获胜的概率为5/9，而小丽获胜的概率为4/9.即游戏A对小华有利，获胜的可能性大于小丽.

　　对游戏B：

　　画树状图或用列表法

所有可能出现的结果共有12种，其中小华抽出的牌面上的数字比小丽大的有5种;根据游戏B的规则，当小丽抽出的牌面上的数字与小华抽到的数字相同或比小华抽到的数字小时，则小丽获胜.所以游戏B小华获胜的概率为5/12，而小丽获胜的概率为7/12.即游戏B对小丽有利，获胜的可能性大于小华.

　　5、(10分)一只箱子里共有3个球，其中2个白球，1个红球，它们除颜色外均相同。

　　(1)从箱子中任意摸出一个球是白球的概率是多少?

　　(2)从箱子中任意摸出一个球，不将它放回箱子，搅匀后再摸出一个球，求两次摸出球的都是白球的概率，并画出树状图。

解：(1)从箱子中任意摸出一个球是白球的概率是

　　(2)记两个白球分别为白1与白2，画树状图如图所示：

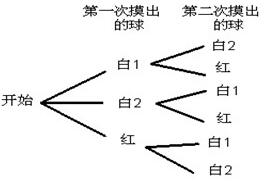
　　从树状图可看出：事件发生的所有可能的结果总数为6，

两次摸出球的都是白球的结果总数为2，因此其概率P=2/6=1/3.

　　6、(10分)汶川地震牵动着全国亿万人民的心，某校为地震灾区开展了“献出我们的爱” 赈灾捐款活动.八年级(1)班50名同学积极参加了这次赈灾捐款活动，下表是小明对全班捐款情况的统计表：

　　因不慎两处被墨水污染，已无法看清，但已知全班平均每人捐款38元.

　　(1)根据以上信息请帮助小明计算出被污染处的数据，并写出解答过程.

　　(2)该班捐款金额的众数、中位数分别是多少?

　　解：(1) 被污染处的人数为11人 。设被污染处的捐款数为x元，则 11x+1460=50×38

　　解得 x=40。

　　答：(1)被污染处的人数为11人，被污染处的捐款数为40元.

　　(2)捐款金额的中位数是40元，捐款金额的众数是50元.