第三节　投资风险报酬

　　一、投资风险与报酬的关系

　　(一)投资风险的含义

　　投资的未来实际报酬偏离预期报酬的可能性。

　　(二)投资风险报酬的含义

　　投资者因承受风险而获得的额外投资报酬，也称投资风险补偿。

　　(三)投资风险与报酬的基本关系

　　投资风险越高，投资者要求的投资风险报酬率就越高，从而投资报酬率也就越高。

　　投资报酬率=无风险投资报酬率+投资风险报酬率

　　二、单项投资风险报酬率的衡量

　　【做题步骤】确定概率及其分布→计算期望报酬率→计算方差、标准离差→计算标准离差率→确定风险报酬系数、计算风险报酬率→计算投资报酬率

　　(一)计算期望报酬率

单项资产期望值:

其中：

代表期望值，Pi表示随机事件的第i种结果，Ki代表该种结果出现的概率

　　【例1-16】某企业有A、B两项投资，其可能的投资报酬率及其概率分布如表1-4所示，试计算这两项投资的期望报酬率。

	投资报酬率		概率分布
实施情况	A项投资	B项投资	A项投资	B项投资
较好	15%	20%	0.20	0.30
一般	10%	15%	0.60	0.40
较差	0	-10%	0.20	0.30

　　正确答案

　　A项投资的期望报酬率为：

　　KA=K1P1+K2P2+K3P3=15%×0.20+10%×0.60+0×0.20=9%

　　B项投资的期望报酬率为：

　　KB=K1P1+K2P2+K3P3=20%×0.30+15%×0.4+(-10%)×0.30=9%

　　(二)计算方差、标准离差

　　方差公式:

     

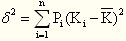
　　标准差公式:

     

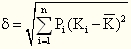
　　【结论】标准差或方差指标衡量的是风险的绝对大小。在预期收益率相等的情况下，标准差或方差越大，则风险越大;标准差或方差越小，则风险越小。因此不适用于比较具有不同预期收益率的资产的风险。

　　【例1-17】根据“例1-16”的资料，试计算A、B两项投资的标准离差。

　　正确答案

　　A项投资的标准离差为：

     

　　B项投资的标准离差为：

     

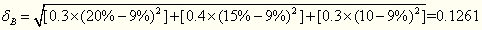
　　(三)计算标准离差率

　　1.公式：标准离差率(V)=标准离差/期望值

　　2.特点：标准离差率是相对指标，它表示某资产每单位预期收益中所包含的风险的大小。一般情况下，标准离差率越大，资产的相对风险越大;标准离差率越小，资产的相对风险越小。可以用来比较预期收益率不同的资产之间的风险大小。

　　【例1-18】某企业有C、D两项投资，期望报酬率分别为20%、15%，标准离差分别为0.198、0.123。C、D两项投资的标准离差率分别计算如下:

　　正确答案Vc=0.198/20%×100%=99%

　　VD=0.123/15%×100%=82%

　　由于C项投资的标准离差率大于D项投资，因此C项投资的风险高于D项投资。

　　【例题·单选题】某企业拟进行一项存在一定风险的完整工业项目投资，有甲、乙两个方案可供选择。甲方案的收益期望值为2000万元，标准离差为600万元;乙方案的收益期望值为2400万元，标准离差为600万元。下列结论中正确的是(　)。

　　A.甲方案的风险大于乙方案

　　B.甲方案的风险小于乙方案

　　C.甲、乙两方案的风险相同

　　D.无法评价甲、乙两方案的风险大小

　　正确答案A

　　答案解析期望值不同应比较标准离差率。

　　甲标准离差率=600/2000=0.3;

　　乙标准离差率=600/2400=0.25。

　　(四)确定风险报酬系数、计算风险报酬率

　　风险报酬率=风险报酬系数×标准离差率

　　(五)确定投资报酬率

　　1.投资报酬率=无风险报酬率+风险报酬率

　　即K = RF+RR = RF+b·V

　　【注意】无风险报酬率通常用国债利率来表示。

　　2.风险越大，风险报酬率也越高，投资人要求的必要报酬率也越高。

　　【例1-19】利用“例1-18”的资料，假定无风险报酬率为10%，C、D两项投资的风险报酬系数分别为5%、4%。这两项投资的风险报酬率和总报酬率分别计算如下：

　　正确答案

　　RRc=5%×99%=4.95%

　　Kc=10%+4.95%=14.95%

　　RRD=4%×82%=3.28%

　　KD=10%+3.28%=13.28%

　　【例题·单选题】某投资项目的标准离差率为75%，风险报酬系数为20%，国债的年利率为5%，则该投资项目的投资报酬率为(　)。

　　A.10%　　　　B.15%

　　C.16%　　　　D.20%

　　正确答案D

　　答案解析投资报酬率=5%+20%×75%=20%。

　　【例题·单选题】甲项目的期望报酬率为20%，标准离差为10%，经测算甲项目的风险报酬系数为0.2，已知无风险报酬率为5%,则甲项目的投资报酬率是(　)。

　　A.20%　　　　B.15%

　　C.10%　　　　D.9%

　　正确答案』B

　　答案解析标准离差率= 标准离差/期望值=10%/20%=50%

　　投资报酬率=无风险报酬率+风险报酬率=无风险报酬率+风险报酬系数×标准离差率=5%+0.2×50%=15%。

　　三、投资组合风险报酬率的衡量

　　(一)投资组合风险类型的分析

类型	定义	特点	例子
可分散风险 （非系统风险）	某些因素引起证券市场上特定证券报酬波动的可能性	通过投资组合能分散	个别公司或资产所特有
不可分散风险（市场风险、系统风险）	某些因素引起证券市场上所有证券报酬波动的可能性	通过投资组合不能分散	战争、经济衰退等

　　1.可分散风险和相关系数

　　相关系数是反映投资组合中不同证券之间风险相关程度的指标。

　　(1)相关系数可以用协方差来计算：

     

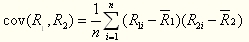
协方差为正	两项资产的收益率呈同方向变化
协方差为负	两项资产的收益率呈反方向变化
协方差为0	两项资产收益率之间不相关

　　【例1-20】某投资组合由S、T两种证券构成，各自的报酬率如表1-5所示。计算两种证券的协方差。

年 份	Rs（%）	RT（%）
20×1	5	25
20×2	15	15
20×3	25	5

　　正确答案

　　首先分别计算S、T两种证券的年度平均报酬率为：

                                                                                                                                                                                                               

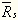
=(5%+15%+25%)/3=15%

=(25%+15%+5%)/3=15%

　　然后计算S、T两种证券的协方差

=

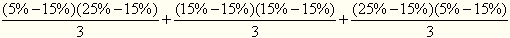
　　=-0.0067

　　(2)相关系数：协方差为绝对数，不便于比较，再者难以解释含义。为克服弊端，提出了相关系数这一指标。

     

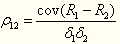
　　【结论】-1≤ρ≤1，相关系数越小，风险分散效果越好

相关系数＝-1	完全负相关，等额投资时可分散风险可以抵消
相关系数＝1	完全正相关，不能抵消风险
相关系数＝0	不相关

　　【例1-21】利用“例1- 20”计算S、T两种证券的相关系数。首先分别计算S、T两种证券的标准离差为：

　　正确答案

     

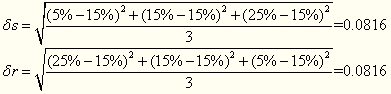
　　然后计算S、T两种证券的相关系数为：

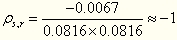
　　2.不可分散风险和贝塔系数

　　(1)不可分散风险通常用贝塔系数来测定。贝塔系数体现市场风险与该证券风险的关系。风险收益率=贝塔系数×市场风险收益率

　　即：贝塔系数=某资产的风险收益率/市场风险收益率

　　(2)分析：

贝塔系数大于1	风险程度高于证券市场
贝塔系数小于1	风险程度低于证券市场
贝塔系数等于1	风险程度等于证券市场

　　(二)投资组合必要报酬率的计算

1.投资组合的贝塔系数

　　2.投资组合的风险报酬率 RP=βp(Rm-RF)

　　其中，Rm为证券市场的平均报酬率，RF为证券市场的无风险报酬率

　　3.投资组合风险必要报酬率=无风险报酬率+风险报酬率

　　即：投资组合的必要报酬率 KP = RF +βP(RM-RF)

　　【总结1】单项投资报酬率计算

1.期望报酬率

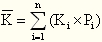
2.标准差

3.标准差率

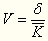
　　4.风险报酬率RR=b(风险报酬率系数)×V

5.总报酬(必要报酬)=Rf+RR = Rf+b·

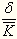
　　【总结2】投资组合报酬率计算

1.分散风险：协方差 COV(R1,R2)→相关系数

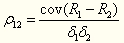
　　2.不可分散β系数

　　(1)投资组合的贝塔系数

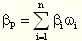
　　(2)投资组合的风险报酬率 RP=βp(Rm-RF)

　　(3)投资组合的必要报酬率 KP = RF +βP(RM-RF)