一、 选择题：本大题共12小题。每小题5分，在每个小题给出的四个选项中，只有一

4. 体积为8的正方体的顶点都在同一球面上，则该球面的表面积为

16.有三张卡片，分别写有1和2，1和3，2和3. 甲，乙，丙三人各取走一张卡片，甲看了乙的卡片后说：“我与乙的卡片上相同的数字不是2”，乙看了丙的卡片后说：“我与丙的卡片上相同的数字不是1”，丙说：“我的卡片上的数字之和不是5”，则甲的卡片上的数字是________________.

【答案】1和3

【解析】由题意分析可知甲的卡片上数字为1和3，乙的卡片上数字为2和3，丙卡片上数字为1和2.

三、解答题：解答应写出文字说明，证明过程或演算步骤．

17．(本小题满分12分)

18． (本小题满分12分)

某险种的基本保费为a（单位：元），继续购买该险种的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下：

随机调查了该险种的200名续保人在一年内的出险情况，得到如下统计表：

（I）记A为事件：“一续保人本年度的保费不高于基本保费”。求P(A)的估计值；

(II)记B为事件：“一续保人本年度的保费高于基本保费但不高于基本保费的160％”.求P(B)的估计值；

（III）求续保人本年度的平均保费估计值.

【试题分析】（I）由已知可得续保人本年度的保费不高于基本保费的频数，进而可得P(A)的估计值；（II）由已知可得续保人本年度的保费高于基本保费但不高于基本保费的160％的频数，进而可得P(B)的估计值；（III）计算出险次数的频率，进而可得续保人本年度的平均保费估计值．

19．（本小题满分12分）

如图，菱形ABCD的对角线AC与BD交于点O，点E、F分别在AD，CD上，AE=CF，EF交BD于点H，将VDEF沿EF折到VD’EF的位置.

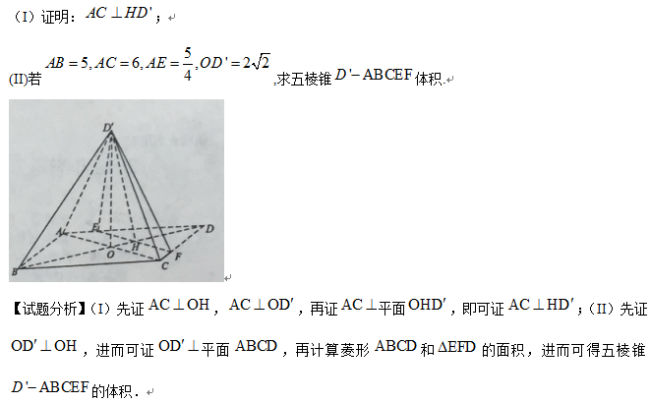
20．（本小题满分12分）

21．（本小题满分12分）

请考生在第22~24题中任选一题作答，如果多做，则按所做的第一题计分.

22．（本小题满分10分）选修4-1：几何证明选讲

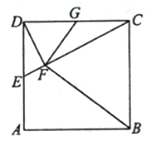
如图，在正方形ABCD中，E，G分别在边DA，DC上（不与端点重合），且DE=DG，过D点作DF⊥CE，垂足为F.

（Ⅰ）证明：B，C，G，F四点共圆；

（Ⅱ）若AB=1，E为DA的中点，求四边形BCGF的面积.